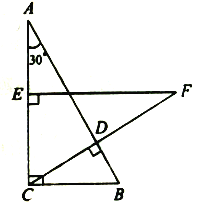
【题目】如图,在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3cm,CD⊥AB,在AC上取一点E,使EC=BC,过点E作EF⊥AC交CD的延长线于点F,求EF和AE的长.
参考答案:
【答案】EF=![]() cm,
cm,![]() cm
cm
【解析】
根据垂直的定义得到∠CEF=∠BCA=90°,再根据等角的余角相等得到∠ECF=∠CBA,则可根据“ASA”可判断△ECF≌△CBA,再根据勾股定理求出AC=EF=![]() cm,然后利用AE=AC-EC进行计算即可.
cm,然后利用AE=AC-EC进行计算即可.
解:∵△ACB和△BDC都是直角三角形
∴∠ACD+∠BCD=90°,∠BCD+∠CBD=90°
∴∠ACD=∠CBD
即∠ECF=∠CBA
在△ECF与△CBA中

∴△ECF≌△CBA(ASA)
∴EF=AC
在Rt△ABC中,∠ACB=90°,∠A=30°,BC=3cm
∴AB=2BC=6cm
∴![]() cm
cm
∴EF=![]() cm,
cm,![]() cm
cm

-
科目: 来源: 题型:
查看答案和解析>>【题目】观察下面三行数
3,9,27,81…①
1,3,9,27…②
2,10,26,82…③
(1)第①行数按什么规律排列?
(2)第②③行数与第①行数分别有什么关系?
(3)设x,y,z分别为第①②③ 行的2019个数,求
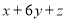 的值
的值 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在梯形ABCD中,AB∥CD.
(1)已知∠A=∠B,求证:AD=BC;
(2)已知AD=BC,求证:∠A=∠B.

-
科目: 来源: 题型:
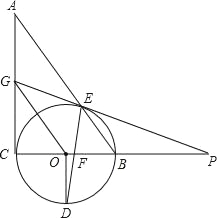
查看答案和解析>>【题目】如图,Rt△ABC中,∠C=90°,以BC为直径的⊙O交AB于E,OD⊥BC交⊙O于D,DE交BC于F,点P为CB延长线上的一点,PE延长交AC于G,PE=PF,下列4个结论:①GE=GC;②AG=GE;③OG∥BE;④∠A=∠P.其中正确的结论是_____(填写所有正确结论的序号)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,点0是AC边上一动点,过点0作DE,使DE∥BC,DE交∠ACB的角平分线于点D,交∠ACB的外角平分线于点E.
(1)求证:OD=OE;
(2)当点0运动到何处时,四边形CDAE是矩形?请证明你的结论.

-
科目: 来源: 题型:
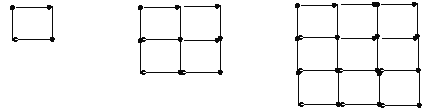
查看答案和解析>>【题目】如图是用火柴棍摆成边长分别是1、2、3根火柴棍时的正方形,当边长为n根火柴棍时,若摆出的正方形所用的火柴棍的根数为S,则S= (用含n的代数式表示,n为正整数).
-
科目: 来源: 题型:
查看答案和解析>>【题目】某学校准备购买A、B两种型号篮球,询问了甲、乙两间学校了解这两款篮球的价格,下表是甲、乙两间学校购买A、B两种型号篮球的情况:
购买学校
购买型号及数量(个)
购买支出款项(元)
A
B
甲
3
8
622
乙
5
4
402
(1)求A、B两种型号的篮球的销售单价;
(2)若该学校准备用不多于1000元的金额购买这两种型号的篮球共20个,求A种型号的篮球最少能采购多少个?
相关试题

