【题目】已知，Rt△ABC中，∠ACB＝90°，AC＝5，BC＝12，点D在边AB上，以AD为直径的⊙O，与边BC有公共点E，则AD的最小值是_____．

【答案】

【解析】

AD的最小值取最小值，则OA最小，而圆与边BC有公共点E，则圆与BC相切时，OA最小，即AD最小.由题意可证△EBO∽△ABC，可得 ，可求OE的长，即可求AD的最小值．

解：当E点是切点且EO⊥BC时，则AD有最小值，如图，


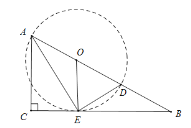
∴OE=OD，
∵AD是直径，
∴∠AED=90°，
∴∠BEO=∠BCA=90°，
∵∠EBO=∠ABC，
∴△EBO∽△ABC，
∴，
∵Rt△ABC中，∠ACB=90°，AC=5，BC=12，
∴AB=13，
设OA=OD=OE=m，
∴，
解得 ，
∴AD=2m=，
∴AD的最小值为，
故答案为，

关闭