【题目】已知:如图,四边形ABCD是菱形,点G是BC延长线上一点,连接AG,分别交BD、CD于点E、F,连接CE。
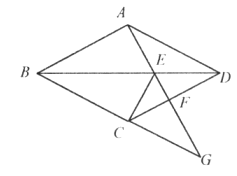
(1)求证:∠DAE=∠DCE; (2)求证:AE2=EF·EG。
参考答案:
【答案】(1)、证明过程见解析;(2)、证明过程见解析
【解析】
试题分析:(1)、根据菱形的性质得出△ADE和△CDE全等,从而得出答案;(2)、根据菱形的性质得出∠DAG=∠G,根据已知条件得出∠DCE=∠G,从而得出△ECF和△EGC相似,结合△ADE和△CDE得出答案.
试题解析:(1)、∵四边形ABCD是菱形 ![]() ,AB∥CD ∴∠ABD=∠ADB,∠ABD=∠CDE,
,AB∥CD ∴∠ABD=∠ADB,∠ABD=∠CDE,
∴∠ADE=∠CDE,AD=CD ![]() ∴△ADE≌△CDE(SAS) ∴∠DAE=∠DCE
∴△ADE≌△CDE(SAS) ∴∠DAE=∠DCE
(2)、∵四边形ABCD是菱形 ∴AD∥BC,∠DAG=∠G ∵∠DAE=∠DCE ∴∠DCE=∠G
∵∠CEF=∠GEC ∴△ECF∽△EGC ![]() ∵△ADE≌△CDE,
∵△ADE≌△CDE,![]()
![]()
-
科目: 来源: 题型:
查看答案和解析>>【题目】某小区2010年屋顶绿化面积为2000平方米,计划2012年屋顶绿化面积要达到2880平方米.如果每年屋顶绿化面积的增长率相同,那么这个增长率是_________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若一个正数的平方根是a-5 和2a-4 ,则这个正数是________ .
-
科目: 来源: 题型:
查看答案和解析>>【题目】2016年我国对“一带一路”沿线国家直接投资145亿美元,将145亿用科学记数法表示为______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】为缓解“停车难”的问题,某单位拟建造地下停车库,建筑设计师提供了该地下车库的设计示意图(如图),按规定,地下车库坡道口上方要张贴限高标志,以便高职停车人车辆能否安全驶入.
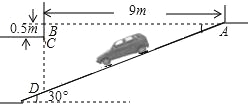
(1)图中线段CD (填“是”或“不是”)表示限高的线段,如果不是,请在图中画出表示限高的线段;
(2)一辆长×宽×高位3916×1650×1465(单位:mm)的轿车欲进入车库停车,请通过计算,判断该汽车能否进入该车库停车?(本小问中
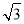 取1.7,精确到0.1)
取1.7,精确到0.1) -
科目: 来源: 题型:
查看答案和解析>>【题目】两个相似多边形的一组对应边分别为3cm和4.5cm,如果它们的面积和为78cm2,那么较大多边形的面积为( )
A. 46.8 cm2 B. 42 cm2 C. 52 cm2 D. 54 cm
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列方程是一元一次方程的是( )
A、x-y=6 B、x–2=x C、x2+3x=1 D、1+x=3
相关试题

