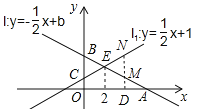
【题目】如图,已知直线![]() :
:![]() 与x轴,y轴的交点分别为A,B,直线
与x轴,y轴的交点分别为A,B,直线![]() :
: ![]() 与y轴交于点C,直线
与y轴交于点C,直线![]() 与直线
与直线![]() 的交点为E,且点E的横坐标为2.
的交点为E,且点E的横坐标为2.
(1)求实数b的值;
(2)设点D(a,0)为x轴上的动点,过点D作x轴的垂线,分别交直线![]() 与直线
与直线![]() 于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.
于点M、N,若以点B、O、M、N为顶点的四边形是平行四边形,求a的值.

参考答案:
【答案】(1)3;(2)a=5或-1.
【解析】
(1)利用一次函数图象上点的坐标特征,由点E在直线![]() 上可得到点E的坐标,由点E在直线
上可得到点E的坐标,由点E在直线![]() 上,进而得出实数b的值;
上,进而得出实数b的值;
(2)依据题意可得MN=|1+![]() a(3
a(3![]() a)|=|a2|,BO=3.当MN=BO=3时,以点B、O、M、N为顶点的四边形为平行四边形,即可得到|a-2|=3,进而得出a的值.
a)|=|a2|,BO=3.当MN=BO=3时,以点B、O、M、N为顶点的四边形为平行四边形,即可得到|a-2|=3,进而得出a的值.
解:(1)∵点E在直线l1上,且点E的横坐标为2,
∴点E的坐标为(2,2),
∵点E在直线l上,
∴2=![]() ×2+b,
×2+b,
解得:b=3;
(2)如图,当x=a时,yM=3![]() a,yN=1+
a,yN=1+![]() a,
a,
∴MN=|1+![]() a(3
a(3![]() a)|=|a2|,
a)|=|a2|,
当x=0时,yB=3,
∴BO=3.
∵BO∥MN,
∴当MN=BO=3时,以点B、O、M、N为顶点的四边形为平行四边形,
此时|a-2|=3,
解得:a=5或a=-1.
∴当以点B、O、M、N为顶点的四边形为平行四边形,a的值为5或-1.
故答案为:(1)3;(2)a=5或-1.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如下图,已知AB是⊙O的直径,点P在BA的延长线上,PD切⊙O于点D,过点B作BE垂直于PD,交PD的延长线于点C,连接AD并延长,交BE于点E.
(1)求证:AB=BE;
(2)若PA=2,cosB=

 ,求⊙O半径的长.
,求⊙O半径的长.
-
科目: 来源: 题型:
查看答案和解析>>【题目】我们规定:将一个平面图形分成面积相等的两部分的直线叫做该平面图形的“等积线”,等积线被 这个平面图形截得的线段叫做该图形的“等积线段”(例如三角形的中线就是三角形的等积线段).已 知菱形的边长为 4,且有一个内角为 60°,设它的等积线段长为 m,则 m 的取值范围是( )
A. m=4 或 m=4
 B. 4≤m≤4
B. 4≤m≤4  C. 2
C. 2  D. 2
D. 2  ≤m≤4
≤m≤4 -
科目: 来源: 题型:
查看答案和解析>>【题目】(Ⅰ)已知|a+3|+(b﹣4)2=0,分别求式子a2+2ab+b2与(a+b)2的值;
(Ⅱ)比较(Ⅰ)中两个式子的计算结果,你能大胆猜想:_____;
(Ⅲ)请你再举一组a,b的值代入计算,验证你的猜想是否正确.
-
科目: 来源: 题型:
查看答案和解析>>【题目】广州火车南站广场计划在广场内种植A,B两种花木共 6600棵,若A花木数量是B花木数量的2倍少600棵.
(1)A,B两种花木的数量分别是多少棵?
(2)如果园林处安排26人同时种植这两种花木,每人每天能种植A花木60棵或B花木40棵,应分别安排多少人种植A花木和B花木,才能确保同时完成各自的任务?
-
科目: 来源: 题型:
查看答案和解析>>【题目】《九章算术》是中国古代数学的重要著作,方程术是它的最高成就,其中记载:今有牛五、羊二,直金十两;牛二、羊五,直金八两。问:牛、羊各直金几何?译文:“假设有 5 头牛、2 只羊,值金 10 两;2 头牛、5 只羊,值金 8 两。问:每头牛、每只羊各值金多少两?” 设每头牛值金 x 两,每只羊值金 y 两,则列方程组错误的是( )
A.
 B.
B. C.
C. D.
D.
-
科目: 来源: 题型:
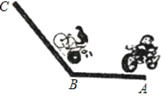
查看答案和解析>>【题目】如图,现有两条乡村公路AB、BC,AB长为1200米,BC长为1600,一个人骑摩托车从A处以20m/s的速度匀速沿公路AB、BC向C处行驶;另一人骑自行车从B处以5m/s的速度从B向C行驶,并且两人同时出发.
(1)求经过多少秒摩托车追上自行车?
(2)求两人均在行驶途中时,经过多少秒两人在行进路线上相距150米?
相关试题

