【题目】连接AB,直线AB与x轴交于点C,与y轴交于点D,平面内有一点E(3,1),直线BE与x轴交于点F.直线AB的解析式记作y1=kx+b,直线BE解析式记作y2=mx+t.求:
(1)直线AB的解析式△BCF的面积;
(2)当x等于多少时,kx+b>mx+t;
当x等于多少时,kx+b<mx+t;
当x等于多少时,kx+b=mx+t;
(3)在x轴上有一动点H,使得△OBH为等腰三角形,求H的坐标.
参考答案:
【答案】解:(1)观察函数图象可知:
点C(﹣4,0),点D(0,2),点B(2,3),
将C、D点坐标代入直线AB的解析式中,得 ![]() ,
,
解得:![]() .
.
∴直线AB的解析式为y1=![]() x+2.
x+2.
将点B(2,3),E(3,1)代入到直线BE的解析式中,得 ![]() ,
,
解得: ![]() .
.
∴直线BE的解析式为y2=﹣2x+7.
令y2=0,则有﹣2x+7=0,解得m=![]() ,
,
即点F的坐标为(![]() ,0).
,0).
∴CF=![]() ﹣(﹣4)=
﹣(﹣4)=![]() ,
,
∴△BCF的面积S=![]() ×3CF=
×3CF=![]() ×3×
×3×![]() =
=![]() .
.
(2)结合函数图象可知:
当x>2时,kx+b>mx+t;当x<2时,kx+b<mx+t;当x=2时,kx+b=mx+t.
故答案为:>2;<2;=2.
(3)设点H的坐标为(n,0).
∵点O(0,0),点B(2,3),
∴OB= ![]() =
=![]() ,OH=|n|,BH=
,OH=|n|,BH=![]() .
.
△OBH为等腰三角形分三种情况:
①当OB=OH时,即![]() =|n|,解得:n=±
=|n|,解得:n=±![]() ,
,
此时点H的坐标为(﹣![]() ,0)或(
,0)或(![]() ,0);
,0);
②当OB=BH时,即![]() =
=![]() ,解得:n=0(舍去),或n=4.
,解得:n=0(舍去),或n=4.
此时点H的坐标为(4,0);
③当OH=BH时,即|n|=![]() ,解得:n=
,解得:n=![]() .
.
此时点H的坐标为(![]() ,0).
,0).
综上可知:点H的坐标为(﹣![]() ,0)、(
,0)、(![]() ,0)、(4,0)或(
,0)、(4,0)或(![]() ,0).
,0).
【解析】(1)根据观察图象可以找出点B、C、D的坐标,根据待定系数法即可求出直线AB、BE的解析式,令y2=0即可求出点F的坐标,结合三角形的面积公式即可得出结论;
(2)当直线AB的图象在直线BE图象上方时,有kx+b>mx+t;当直线AB的图象在直线BE图象下方时,有kx+b<mx+t;二者相交时,有kx+b=mx+t.结合图象即可得出结论;
(3)设点H的坐标为(n,0),用两点间的距离公式找出OB、OH、BH的长度,结合△OBH为等腰三角形的三种情况,即可求出n的值.
-
科目: 来源: 题型:
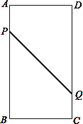
查看答案和解析>>【题目】如图,在矩形ABCD中,AB=16cm,BC=6cm,点P从A出发沿AB以3cm/s的速度向点B移动,一直到达点B为止;同时,点Q从点C出发沿以2cm/s的速度向点D移动.经过多长时间P、Q两点的距离是10?
-
科目: 来源: 题型:
查看答案和解析>>【题目】收集和整理数据.
某中学七(1)班学习了统计知识后,数学老师要求每个学生就本班学生的上学方式进行一次全面调查,如图是一同学通过收集数据后绘制的两幅不完整的统计图,请根据图中提供的信息,解答下列问题:(每个学生只选择1种上学方式).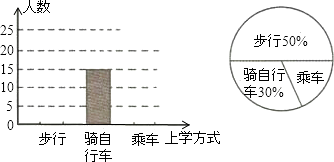
(1)求该班乘车上学的人数;
(2)将频数分布直方图补充完整;
(3)若该校七年级有1200名学生,能否由此估计出该校七年级学生骑自行车上学的人数,为什么? -
科目: 来源: 题型:
查看答案和解析>>【题目】小武新家装修,在装修客厅时,购进彩色地砖和单色地砖共100块,共花费5600元.已知彩色地砖的单价是80元/块,单色地砖的单价是40元/块.
(1)两种型号的地砖各采购了多少块?
(2)如果厨房也要铺设这两种型号的地砖共60块,且采购地砖的费用不超过3200元,那么彩色地砖最多能采购多少块? -
科目: 来源: 题型:
查看答案和解析>>【题目】若是关于x的一元二次方程(m﹣1)x2+x+|m|﹣1=0有的一个根为0,则m的值是
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图是常见的安全标记,其中是轴对称图形的是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△DEF中,DE=17cm,EF=30cm,EF边上的中线DG=8cm.
求证:△DEF是等腰三角形.
相关试题

