【题目】定义：若中，其中一个内角是另一个内角的一半，则称为“半角三角形”．

（1）若为半角三角形，，则其余两个角的度数为 ．

（2）如图1，在平行四边形中，，点在边上，以为折痕，将向上翻折，点恰好落在边上的点，若，求证：为半角三角形；

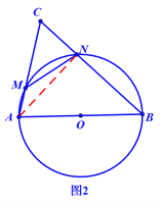
（3）如图2，以的边为直径画圆，与边交于，与边交于，已知的面积是面积的倍．

①求证：．

②若是半角三角形，，直接写出的取值范围．

【答案】（1）45°，45°或30°，60°；（2）见解析；（3）①见解析，②0≤BN≤3

【解析】

（1）根据半角三角形的定义，直接求出其余两个角的度数，即可；

（2）由平行四边形的性质得：∠D＝108°，由翻折可知：∠EFB＝72°，从而得∠EFD＝18°，∠DEF=54°，进而即可得到结论；

（3）①如图2中，连接AN，易得△CMN∽△CBA，从而得＝，由锐角三角函数的定义，即可sin∠CAN＝，进而即可得到结论；②由题意得：△ABC是半角三角形，∠B＝30°或90°时，BN取得最值，进而即可求解．

（1）∵Rt△ABC为半角三角形，∠A＝90°，

∴∠B＝∠C＝45°，或∠B＝60°，∠C＝30°或∠B＝30°，∠C＝60°，

∴其余两个角的度数为45°，45°或30°，60°，

故答案为45°，45°或30°，60°；

（2）如图1中，∵平行四边形ABCD中，∠C＝72°，

∴∠D＝108°，

由翻折可知：∠EFB＝∠C＝72°，

∵，

∴∠EFD＝18°，

∴∠DEF＝180°-108°-18°=54°，

∴∠DEF＝∠D，即△DEF是半角三角形；

（3）①如图2中，连接AN．

∵AB是直径，

∴∠ANB＝90°，

∵∠C＝∠C，∠CMN＝∠B，

∴△CMN∽△CBA，

∴（）2＝=，即＝，

∵在Rt△ACN中，sin∠CAN＝＝，

∴∠CAN＝30°，

∴∠C＝60°；

②∵△ABC是半角三角形，∠B＝30°或90°时，BN取得最值，

∴0≤BN≤3．

关闭