【题目】如图,矩形ABCD的对角线AC,BD相交于点O,∠ACB=30°,BC=3,分别过点B,C作BE∥AC,CE∥BD,且BE,CE相交于点E. 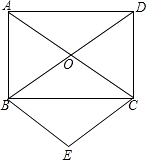
(1)求AB,AC的长;
(2)判断四边形BOCE的形状.
参考答案:
【答案】
(1)解:∵四边形ABCD是矩形,
∴∠ABC=90°,且∠ACB=30°,
∴AC=2AB,
设AB=x,则AC=2x,在Rt△ABCD中,由勾股定理可得x2+32=(2x)2,解得x= ![]() 或x=﹣
或x=﹣ ![]() (舍去),
(舍去),
∴AB= ![]() ,AC=2
,AC=2 ![]()
(2)解:四边形BOCE是菱形,理由如下:
∵BE∥AC,CE∥BD,
∴四边形BOCE是平行四边形,
∵四边形ABCD是矩形,
∴AO=CO,BO=DO,AC=BD,
∴BO=CO,
∴四边形BOCE是菱形
【解析】(1)由矩形的性质可△ABC为直角三角形,由条件结合勾股定理可求得AB、AC的长;(2)由条件可先判定四边形BOCE为平行四边形,再结合矩形的性质可判定其为菱形.
【考点精析】解答此题的关键在于理解菱形的判定方法的相关知识,掌握任意一个四边形,四边相等成菱形;四边形的对角线,垂直互分是菱形.已知平行四边形,邻边相等叫菱形;两对角线若垂直,顺理成章为菱形,以及对矩形的性质的理解,了解矩形的四个角都是直角,矩形的对角线相等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一些图书分给某班学生阅读,如果每人分4本,则剩余23本;如果每人分5本,则还缺22本,这个班有学生( )
A. 45名B. 50名C. 55名D. 60名
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知函数
 (a是常数,a≠0),下列结论正确的是( )
(a是常数,a≠0),下列结论正确的是( )A.当a=1时,函数图象经过点(﹣1,1)
B.当a=﹣2时,函数图象与x轴没有交点
C.若a<0,函数图象的顶点始终在x轴的下方
D.若a>0,则当x≥1时,y随x的增大而增大
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,直线
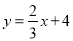 与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )
与x轴、y轴分别交于点A和点B,点C、D分别为线段AB、OB的中点,点P为OA上一动点,PC+PD值最小时点P的坐标为( )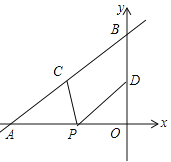
A.(﹣3,0) B.(﹣6,0) C.(
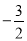 ,0) D.(
,0) D.( ,0)
,0) -
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:a2b+2ab2+b3= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】﹣2x2y4的系数是a,次数是b,则a+b=_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在数轴上表示﹣2的点与表示3的点之间的距离是( )
A.5
B.﹣5
C.1
D.﹣1
相关试题

