Question

【题目】如图，在△ABC中，AD是BC边上的中线，E是AD的中点，过点A作BC的平行线交BE的延长线于点F，连接CF．

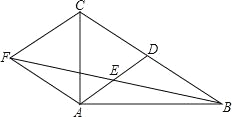
（1）求证：AF=DC；

（2）若AB⊥AC，试判断四边形ADCF的形状，并证明你的结论．

Answer 1

【答案】(1)证明见解析；（2）四边形ADCF是菱形，证明见解析.

【解析】

试题分析：（1）根据AAS证△AFE≌△DBE，推出AF=BD，即可得出答案；

（2）得出四边形ADCF是平行四边形，根据直角三角形斜边上中线性质得出CD=AD，根据菱形的判定推出即可．

试题解析：（1）∵AF∥BC，

∴∠AFE=∠DBE，

∵E是AD的中点，AD是BC边上的中线，

∴AE=DE，BD=CD，

在△AFE和△DBE中

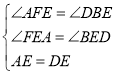
∴△AFE≌△DBE（AAS），

∴AF=BD，

∴AF=DC．

（2）四边形ADCF是菱形，

证明：AF∥BC，AF=DC，

∴四边形ADCF是平行四边形，

∵AC⊥AB，AD是斜边BC的中线，

∴AD=BC=DC，

∴平行四边形ADCF是菱形．