【题目】如图,已知数轴上点A表示的数为6,点B表示的数为﹣4,C为线段AB的中点,动点P从点B出发,以每秒2个单位长度的速度沿数轴向右匀速运动,设运动时间为t(t>0)秒.
![]()
(1)点C表示的数是 ;
(2)当t= 秒时,点P到达点A处;
(3)点P表示的数是 (用含字母t的代数式表示);
(4)当t= 秒时,线段PC的长为2个单位长度;
(5)若动点Q同时从点A出发,以每秒1个单位长度的速度沿数轴向左匀速运动,那么,当t= 秒时,PQ的长为1个单位长度.
参考答案:
【答案】(1)1;(2)5;(3)2t﹣4;(4)1.5秒或3.5秒;(5)3秒或![]() 秒.
秒.
【解析】
试题分析:(1)根据线段中点坐标公式可求点C表示的数;
(2)根据时间=路程÷速度,可求t的值;
(3)根据两点之间的距离公式可求点P表示的数;
(4)分P在点C左边和点C右边两种情况讨论求解;
(5)分点P、Q相遇前和点P、Q相遇后两种情况讨论求解.
解:(1)(6﹣4)÷2
=2÷2
=1.
故点C表示的数是1.
故答案为:1;
(2)[6﹣(﹣4)]÷2
=10÷2
=5(秒).
答:当t=5秒时,点P到达点A处.
故答案为:5;
(3)点P表示的数是2t﹣4.
故答案为:2t﹣4;
(4)P在点C左边,
[1﹣2﹣(﹣4)]÷2
=3÷2
=1.5(秒).
P在点C右边,
[1+2﹣(﹣4)]÷2
=7÷2
=3.5(秒).
答:当t=1.5秒或3.5秒秒时,线段PC的长为2个单位长度.
故答案为:1.5秒或3.5秒;
(5)点P、Q相遇前,依题意有
(2+1)t=6﹣(﹣4)﹣1,
解得t=3;
点P、Q相遇后,依题意有
(2+1)t=6﹣(﹣4)+1,
解得t=![]() .
.
答:当t=3秒或![]() 秒秒时,PQ的长为1个单位长度.
秒秒时,PQ的长为1个单位长度.
故答案为:3秒或![]() 秒.
秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把一副三角尺ABC与BDE按如图所示那样拼在一起,其中A、B、D三点在同一直线上,BM为∠CBE的平分线,BN为∠DBE的平分线,则∠MBN的度数是( )
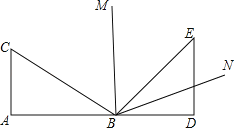
A.60° B.67.5° C.75° D.85°
-
科目: 来源: 题型:
查看答案和解析>>【题目】若﹣2amb4与3a2bn+2是同类项,则m+n= .
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知△ABC中,a、b、c分别是∠A、∠B、∠C的对边,下列条件不能判断△ABC是直角三角形的是( )
A.∠A﹣∠B=∠C
B.∠A:∠B:∠C=3:4:5
C.(b+c)(b﹣c)=a2
D.a=7,b=24,c=25
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图所示,直线l是四边形ABCD的对称轴,若AB=CD,有下面4个结论:
①AB∥CD;②AC⊥BD;③AO=CO;④AB⊥BC.
其中正确的结论有几个( )
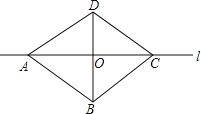
A.4个 B.3个 C.2个 D.1个
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知抛物线y=﹣
 x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
x2+bx+c与坐标轴分别交于点A(0,8)、B(8,0)和点E,动点C从原点O开始沿OA方向以每秒1个单位长度移动,动点D从点B开始沿BO方向以每秒1个单位长度移动,动点C、D同时出发,当动点D到达原点O时,点C、D停止运动.
(1)直接写出抛物线的解析式: ;
(2)求△CED的面积S与D点运动时间t的函数解析式;当t为何值时,△CED的面积最大?最大面积是多少?
(3)当△CED的面积最大时,在抛物线上是否存在点P(点E除外),使△PCD的面积等于△CED的最大面积?若存在,求出P点的坐标;若不存在,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系中,已知ABCD的三个顶点坐标分别是A(m,n),B(2,﹣1),C(﹣m,﹣n),则点D的坐标是( )
A.(﹣2,1) B.(﹣2,﹣1) C.(﹣1,﹣2) D.(﹣1,2)
相关试题

