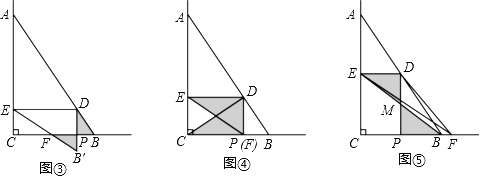
【题目】如图，∠C=90°，点A、B在∠C的两边上，CA=30，CB=20，连结AB．点P从点B出发，以每秒4个单位长度的速度沿BC方向运动，到点C停止．当点P与B、C两点不重合时，作PD⊥BC交AB于D，作DE⊥AC于E．F为射线CB上一点，且∠CEF=∠ABC．设点P的运动时间为x（秒）．

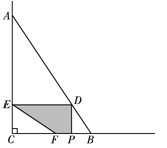
（1）用含有x的代数式表示CE的长；

（2）求点F与点B重合时x的值；

（3）当点F在线段CB上时，设四边形DECP与四边形DEFB重叠部分图形的面积为y（平方单位）．求y与x之间的函数关系式；

（4）当x为某个值时，沿PD将以D、E、F、B为顶点的四边形剪开，得到两个图形，用这两个图形拼成不重叠且无缝隙的图形恰好是三角形．请直接写出所有符合上述条件的x值．

【答案】（1）6x；（2），（3）y=（5-x）2；（4）；；．

【解析】

试题（1）首先证明△ABC∽△DBP∽△FEC，即可得出比例式进而得出表示CE的长；

（2）根据当点F与点B重合时，FC=BC，即可得出答案；

（3）首先证明Rt△DOE∽Rt△CEF，得出，即可得出y与x之间的函数关系式；

（4）根据三角形边长相等得出答案．

试题解析：（1）∵∠C=90°，PD⊥BC，

∴DP∥AC，

∴△DBP∽△ABC，四边形PDEC为矩形，

CE=PD．．

∴．

∴CE=6x；

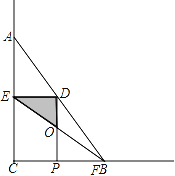
（2）∵∠CEF=∠ABC，∠C为公共角，

∴△CEF∽△CBA，

∴．

∴．

当点F与点B重合时，CF=CB，9x=20．

解得．

（3）当点F与点P重合时，BP+CF=CB，4x+9x=20，

解得．

当时，

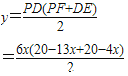
=-51x2+120x．当＜x≤时，

==（20-4x）2．

（或）

（4）①如图③，当PD=PF时，6x=20-13x，解得：x=；△B′DE为拼成的三角形；

②如图④当点F与点P重合时，4x+9x=20，解得：x=；△BDC为拼成的三角形；

③如图⑤，当DE=PB，20-4x=4x，解得：x=，△DPF为拼成的三角形．

关闭