【题目】如图,已知正方形ABCD中,边长为10厘米,点E在AB边上,BE=6厘米.
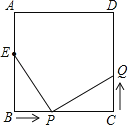
(1)如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CD上由C点向D点运动.
①若点Q的运动速度与点P的运动速度相等,经过1秒后,△BPE与△CQP是否全等,请说明理由;
②若点Q的运动速度与点P的运动速度不相等,当点Q的运动速度为多少时,能够使△BPE与△CQP全等?
(2)若点Q以②中的运动速度从点C出发,点P以原来的运动速度从点B同时出发,都逆时针沿正方形ABCD四边运动,求经过多长时间点P与点Q第一次在正方形ABCD边上的何处相遇?
参考答案:
【答案】(1)点P,点Q运动的时间t=![]() 秒,∴vq=
秒,∴vq=![]() =4.8厘米/秒.
=4.8厘米/秒.
(2)经过![]() 秒点P与点Q第一次在A点相遇.
秒点P与点Q第一次在A点相遇.
【解析】
试题分析:正方形的四边相等,四个角都是直角.(1)①速度相等,运动的时间相等,所以距离相等,根据全等三角形的判定定理可证明.②因为运动时间一样,运动速度不相等,所以BP≠CQ,只有BP=CP时才相等,根据此可求解.
(2)知道速度,知道距离,这实际上是个追及问题,可根据追及问题的等量关系求解.
试题解析(1)①∵t=1秒,∴BP=CQ=4×1=4厘米,∵正方形ABCD中,边长为10厘米,∴PC=BE=6厘米,又∵正方形ABCD,∴∠B=∠C,∴△BPE≌△CQP.
②∵VP≠VQ,∴BP≠CQ,又∵△BPE≌△CQP,∠B=∠C,则BP=PC,而BP=4t,CP=10-4t,
∴4t=10-4t,∴点P,点Q运动的时间t=![]() 秒,∴vq=
秒,∴vq=![]() =4.8厘米/秒.
=4.8厘米/秒.
(2)设经过x秒后点P与点Q第一次相遇,由题意,得4.8x-4x=30,解得x=![]() 秒.
秒.
∴点P共运动了![]() ×4=150厘米,∴点P、点Q在A点相遇,
×4=150厘米,∴点P、点Q在A点相遇,
∴经过![]() 秒点P与点Q第一次在A点相遇.
秒点P与点Q第一次在A点相遇.
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列事件中是必然事件的是( )
A.明天是晴天
B.打开电视,正在播放广告
C.两个负数的和是正数
D.三角形三个内角的和是180° -
科目: 来源: 题型:
查看答案和解析>>【题目】在扇形统计图中,其中一个扇形的中心角为72°,则这个扇形所表示的部分占总体的百分数为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】先化简,再求值:(﹣12x2﹣4xy)﹣2(5xy﹣8x2),其中x=﹣1,y=0.4.
-
科目: 来源: 题型:
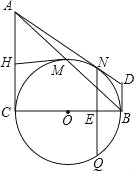
查看答案和解析>>【题目】如图,在Rt△ABC中,∠C=90°,以BC为直径的⊙O交斜边AB于点M,若H是AC的中点,连接MH.
(1)求证:MH为⊙O的切线.
(2)若MH=
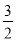 ,tan∠ABC=
,tan∠ABC=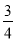 ,求⊙O的半径.
,求⊙O的半径.(3)在(2)的条件下分别过点A、B作⊙O的切线,两切线交于点D,AD与⊙O相切于N点,过N点作NQ⊥BC,垂足为E,且交⊙O于Q点,求线段NQ的长度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB是⊙O的弦,点C为半径OA的中点,过点C作CD⊥OA交弦AB于点E,连接BD,且DE=DB.
(1)判断BD与⊙O的位置关系,并说明理由;
(2)若CD=15,BE=10,tanA=
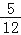 ,求⊙O的直径.
,求⊙O的直径.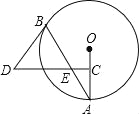
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,以BC为直径的圆交AC于点D,∠ABD=∠ACB.
(1)求证:AB是圆的切线;
(2)若点E是BC上一点,已知BE=4 ,tan∠AEB=,AB∶BC=2∶3,求圆的直径.

相关试题

