25、已知一个角的两边与另一个角的两边分别平行,结合下图,试探索这两个角之间的关系,并说明你的结论.
(1)如图1,AB∥EF,BC∥DE.∠1与∠2的关系是:
(2)如图2,AB∥EF,BC∥DE.∠1与∠2的关系是:
(3)由(1)(2)你得出的结论是:如果
(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角度数的分别是

(1)如图1,AB∥EF,BC∥DE.∠1与∠2的关系是:
∠1=∠2
,理由:如果一个角的两边与另一个角的两边分别平行,
那么这两个角相等
;那么这两个角相等
(2)如图2,AB∥EF,BC∥DE.∠1与∠2的关系是:
∠1=∠2
,理由:如果一个角的两边与另一个角的两边分别平行,
那么这两个角相等
.那么这两个角相等
(3)由(1)(2)你得出的结论是:如果
一个角的两边与另一个角的两边分别平行
,那么
这两个角相等
.(4)若两个角的两边互相平行,且一个角比另一个角的2倍少30°,则这两个角度数的分别是
30°、30°

分析:(1)由已知AB∥EF,BC∥DE,根据平行线的性质得:∠3=∠1,∠3=∠2⇒∠1=∠2.
(2)由已知AB∥EF,BC∥DE,得:∠3=∠1,∠3=∠2⇒∠1=∠2.
(3)由(1)和(2)得出结论如果一个角的两边与另一个角的两边分别平行,那么这两个角相等.
(4)由(3)得出的结论设一个角为x°,列方程求解.
(2)由已知AB∥EF,BC∥DE,得:∠3=∠1,∠3=∠2⇒∠1=∠2.
(3)由(1)和(2)得出结论如果一个角的两边与另一个角的两边分别平行,那么这两个角相等.
(4)由(3)得出的结论设一个角为x°,列方程求解.
解答:解:(1)∠1=∠2,理由:∵AB∥EF
∴∠3=∠2,
∵BC∥DE
∴∠3=∠1
∴∠1=∠2.
故答案为:∠1=∠2,如果一个角的两边与另一个角的两边分别平行,
那么这两个角相等.
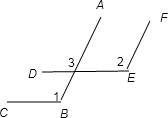

(2)∠1=∠2,理由:∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2.
故答案为:∠1=∠2,如果一个角的两边与另一个角的两边分别平行,
那么这两个角相等.
(3)由(1)(2)我们得到:如果一个角的两边与另一个角的两边分别平行,
那么这两个角相等.
(4)设另一个角为x°,根据以上结论得:
2x-30=x
解得:x=30
故答案为:30°、30°.
∴∠3=∠2,
∵BC∥DE
∴∠3=∠1
∴∠1=∠2.
故答案为:∠1=∠2,如果一个角的两边与另一个角的两边分别平行,
那么这两个角相等.


(2)∠1=∠2,理由:∵AB∥EF,
∴∠3=∠2,
∵BC∥DE,
∴∠3=∠1,
∴∠1=∠2.
故答案为:∠1=∠2,如果一个角的两边与另一个角的两边分别平行,
那么这两个角相等.
(3)由(1)(2)我们得到:如果一个角的两边与另一个角的两边分别平行,
那么这两个角相等.
(4)设另一个角为x°,根据以上结论得:
2x-30=x
解得:x=30
故答案为:30°、30°.
点评:此题考查的知识点视平线的性质,关键是由平行线的性质推出结论.

