【题目】如图的矩形ABCD中,E点在CD上,且AE<AC.若P、Q两点分别在AD、AE上,AP:PD=4:1,AQ:QE=4:1,直线PQ交AC于R点,且Q、R两点到CD的距离分别为q、r,则下列关系何者正确?( ) 
A.q<r,QE=RC
B.q<r,QE<RC
C.q=r,QE=RC
D.q=r,QE<RC
参考答案:
【答案】D
【解析】解:∵在矩形ABCD中,AB∥CD,
∵AP:PD=4:1,AQ:QE=4:1,
∴ ![]() ,
,
∴PQ∥CD,
∴ ![]() =4,
=4,
∵平行线间的距离相等,
∴q=r,
∵ ![]() =4,∴
=4,∴ ![]() =
= ![]() ,
,
∵AE<AC,
∴QE<CR.
故选D.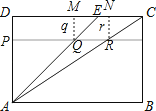
根据矩形的性质得到AB∥CD,根据已知条件得到 ![]() ,根据平行线分线段成比例定理得到PQ∥CD,
,根据平行线分线段成比例定理得到PQ∥CD, ![]() =4,根据平行线间的距离相等,得到q=r,证得
=4,根据平行线间的距离相等,得到q=r,证得 ![]() =
= ![]() ,于是得到结论.本题考查了平行线分线段成比例定理,矩形的性质,熟练掌握平行线分线段成比例定理是解题的关键.
,于是得到结论.本题考查了平行线分线段成比例定理,矩形的性质,熟练掌握平行线分线段成比例定理是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知 A=3x2+3y2﹣2xy,B=xy﹣2y2﹣2x2.
求:(1)2A﹣3B.
(2)若|2x﹣3|=1,y2=9,|x﹣y|=y﹣x,求 2A﹣3B 的值.
(3)若 x=2,y=﹣4 时,代数式 ax3
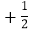 by+5=17,那么当 x=﹣4,y=﹣
by+5=17,那么当 x=﹣4,y=﹣ 时,求代 数式 3ax﹣24by3+6 的值.
时,求代 数式 3ax﹣24by3+6 的值. -
科目: 来源: 题型:
查看答案和解析>>【题目】某房地产开发商 2010 年 6 月从银行贷款 3 亿元开发某楼盘,贷款 期限为两年,贷款年利率为 8%.该楼盘有 A、B 两种户型共计 500 套房,算 上土地成本、建筑成本及销售成本,A 户型房平均每平方米成本为 0.6 万元,
B 户型房平均每平方米成本为 0.7 万元,表是开发商原定的销控表:
销售面积(m2)
销售价格(万元/m2)
A 户型
75
0.8
B 户型
100
1
(1)该楼盘两种户型房各有多少套?
(2)由于限购政策的实施,2011 年以来房地产市场萎靡不振,开发商又急于在两年贷款期限到之前把房卖完,2012 年 1 月实际开盘时将 A 户型房按原定销 售价打 9 折,B 户型房按原定销售价打 8.3 折出售,结果 2012 年 6 月前将两 种户型的房全部卖完,开发商在还完贷款及贷款利息之后,还获利多少万元? 实际销售额比原定销售额下降了百分之几?
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知数轴上有A、B两个点.
(1)如图1,若AB=a,M是AB的中点,C为线段AB上的一点,且
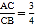 ,则AC= ,CB= ,MC= (用含a的代数式表示);
,则AC= ,CB= ,MC= (用含a的代数式表示);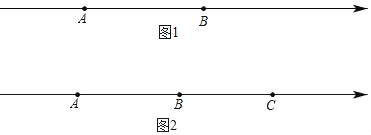
(2)如图2,若A、B、C三点对应的数分别为﹣40,﹣10,20.
①当A、C两点同时向左运动,同时B点向右运动,已知点A、B、C的速度分别为8个单位长度/秒、4个单位长度/秒、2个单位长度/秒,点M为线段AB的中点,点N为线段BC的中点,在B、C相遇前,在运动多少秒时恰好满足:MB=3BN.
②现有动点P、Q都从C点出发,点P以每秒1个单位长度的速度向终点A移动;当点P移动到B点时,点Q才从C点出发,并以每秒3个单位长度的速度向左移动,且当点P到达A点时,点Q也停止移动(若设点P的运动时间为t).当PQ两点间的距离恰为18个单位时,求满足条件的时间t值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,有一内部装有水的直圆柱形水桶,桶高20公分;另有一直圆柱形的实心铁柱,柱高30公分,直立放置于水桶底面上,水桶内的水面高度为12公分,且水桶与铁柱的底面半径比为2:1.今小贤将铁柱移至水桶外部,过程中水桶内的水量未改变,若不计水桶厚度,则水桶内的水面高度变为多少公分?( )

A.4.5
B.6
C.8
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】表为小洁打算在某电信公司购买一支MAT手机与搭配一个门号的两种方案.此公司每个月收取通话费与月租费的方式如下:若通话费超过月租费,只收通话费;若通话费不超过月租费,只收月租费.若小洁每个月的通话费均为x元,x为400到600之间的整数,则在不考虑其他费用并使用两年的情况下,x至少为多少才会使得选择乙方案的总花费比甲方案便宜?( )
甲方案
乙方案
门号的月租费(元)
400
600
MAT手机价格(元)
15000
13000
注意事项:以上方案两年内不可变更月租费
A.500
B.516
C.517
D.600 -
科目: 来源: 题型:
查看答案和解析>>【题目】(1)计算:﹣3﹣(﹣5)+(﹣6)﹣(﹣3);
(2)计算:﹣23+(﹣4)×[(﹣1)2015+(﹣
 )2];
)2];(3)解方程:2x﹣(2﹣x)=4
(4)解方程:2﹣
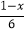 =
= ;
;
相关试题

