搜索
【题目】为响应“书香校响园”建设的号召，在全校形成良好的阅读氛围，随机调查了部分学生平均每天阅读时间，统计结果如图所示，则本次调查中阅读时间为的众数和中位数分别是（ ）
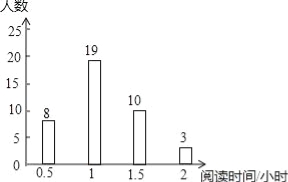
A．2和1 B．1.25和1 C．1和1 D．1和1.25
参考答案：
【答案】C
【解析】
试题分析：给定n个数据，按从小到大排序，如果n为奇数，位于中间的那个数就是中位数；如果n为偶数，位于中间两个数的平均数就是中位数．任何一组数据，都一定存在中位数的，但中位数不一定是这组数据里的数；给定一组数据，出现次数最多的那个数，称为这组数据的众数．如果一组数据存在众数，则众数一定是数据集里的数．由统计图可知阅读时间为1小数的有19人，人数最多，所以众数为1小时；总人数为40，得到中位数应为第20与第21个的平均数，而第20个数和第21个数都是1（小时），即可确定出中位数为1小时．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在平面直角坐标系中，矩形OCDE的顶点C和E分别在y轴的正半轴和x轴的正半轴上，OC=8，OE=17，抛物线y=
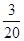x2﹣3x+m与y轴相交于点A，抛物线的对称轴与x轴相交于点B，与CD交于点K．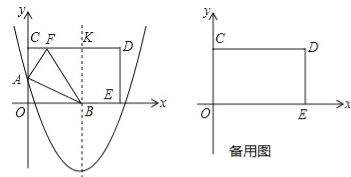
（1）将矩形OCDE沿AB折叠，点O恰好落在边CD上的点F处．
①点B的坐标为（ 、 ），BK的长是 ，CK的长是 ；
②求点F的坐标；
③请直接写出抛物线的函数表达式；
（2）将矩形OCDE沿着经过点E的直线折叠，点O恰好落在边CD上的点G处，连接OG，折痕与OG相交于点H，点M是线段EH上的一个动点（不与点H重合），连接MG，MO，过点G作GP⊥OM于点P，交EH于点N，连接ON，点M从点E开始沿线段EH向点H运动，至与点N重合时停止，△MOG和△NOG的面积分别表示为S1和S2，在点M的运动过程中，S1S2（即S1与S2的积）的值是否发生变化？若变化，请直接写出变化范围；若不变，请直接写出这个值．
温馨提示：考生可以根据题意，在备用图中补充图形，以便作答．
-
科目： 来源： 题型：
查看答案和解析>>【题目】某种衬衫的进价为400元，出售时标价为550元，由于换季，商店准备打折销售，但要 保持利润不低于10%，那么至多打（ ）
A. 6折B. 7折C. 8折D. 9折
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在△ABC中，以AB为直径的⊙O分别与BC，AC相交于点D，E，BD=CD，过点D作⊙O的切线交边AC于点F.
(1)求证：DF⊥AC；
(2)若⊙O的半径为5，∠CDF=30°，求
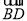的长(结果保留π)．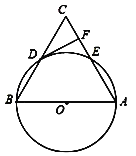
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列说法不正确的是( )
A. 四边都相等的四边形是平行四边形
B. 两组对角分别相等的四边形是平行四边形
C. 对角线互相垂直的四边形是平行四边形
D. 两组对边分别平行的四边形是平行四边形
-
科目： 来源： 题型：
查看答案和解析>>【题目】体育课上，老师测量跳远成绩的主要依据是（ ）
A. 垂线段最短 B. 两点之间，线段最短
C. 平行线间的距离相等 D. 两点确定一条直线
-
科目： 来源： 题型：
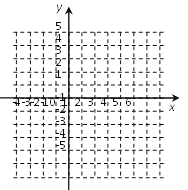
查看答案和解析>>【题目】在平面直角坐标系中，O为坐标原点，已知A（0，a），B（b，b），C（c，a），其中a，b满足关系式|a-4|+ (b-2)2=0，c=a+b.
（1）求A、B、C三点的坐标，并在坐标系中画出△ABC；
（2）如果在第四象限内有一点P（2，m），请用含m的代数式表示三角形CPO的面积.
相关试题
