搜索
【题目】若点M（m﹣3，m+1）在平面直角坐标系的y轴上，则点M的坐标为 ．
参考答案：
【答案】（0，4）
【解析】解：∵点M（m﹣3，m+1）在平面直角坐标系的y轴上， ∴m﹣3=0，
解得m=3，
∴m+1=3+1=4，
∴点M的坐标为（0，4）．
所以答案是：（0，4）．
-
科目： 来源： 题型：
查看答案和解析>>【题目】下列各语句：①对顶角相等吗？②延长线段AB；③内错角相等；④垂线段最短．其中真命题有（ ）
A.1个
B.2个
C.3个
D.4个 -
科目： 来源： 题型：
查看答案和解析>>【题目】若3﹣a和2a+3都是某正数的平方根，则某数为_____．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如果某一个数的一个平方根是﹣3，那么这个数是 ．
-
科目： 来源： 题型：
查看答案和解析>>【题目】若点A（m，n）和点B（5，﹣7）关于x轴对称，则m+n的值是（ ）
A. 2 B. ﹣2 C. 12 D. ﹣12
-
科目： 来源： 题型：
查看答案和解析>>【题目】我校为组织八年级的234名同学去看电影，租用了某公交公司的几辆公共汽车．如果每辆车坐30人，则最后一辆车不空也不满．他们共租了___辆公共汽车．
-
科目： 来源： 题型：
查看答案和解析>>【题目】（1）问题背景
如图①，BC是⊙O的直径，点A在⊙O上，AB=AC，P为BmC上一动点（不与B，C重合），求证：
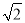PA=PB+PC．小明同学观察到图中自点A出发有三条线段AB，AP，AC，且AB=AC，这就为旋转作了铺垫．于是，小明同学有如下思考过程：
第一步：将△PAC绕着点A顺时针旋转90°至△QAB（如图①）；
第二步：证明Q，B，P三点共线，进而原题得证．
请你根据小明同学的思考过程完成证明过程．
（2）类比迁移
如图②，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB=AC，AB⊥AC，垂足为A，求OC的最小值．
（3）拓展延伸
如图③，⊙O的半径为3，点A，B在⊙O上，C为⊙O内一点，AB=
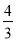AC，AB⊥AC，垂足为A，则OC的最小值为 ．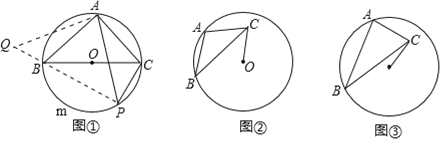
相关试题
