【题目】如图1,将两块全等的直角三角形纸片△ABC和△DEF叠放在一起,其中∠ACB=∠E=90°,BC=DE=6,AC=FE=8,顶点D与边AB的中点重合.
(1)若DE经过点C,DF交AC于点G,求重叠部分(△DCG)的面积;
(2)合作交流:“希望”小组受问题(1)的启发,将△DEF绕点D旋转,使DE⊥AB交AC于点H,DF交AC于点G,如图2,求重叠部分(△DGH)的面积.
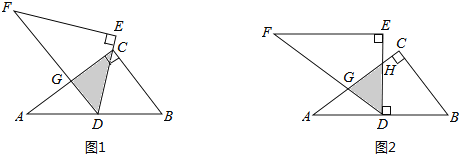
参考答案:
【答案】6; ![]() .
.
【解析】试题分析:(1)、根据题意得出△ABC和△FDE全等,从而得出CG和DG的大小,然后根据三角形的面积计算法则求出三角形的面积;(2)、根据题意得出△ABC和△FDE全等,根据Rt△ABC的勾股定理求出AB的长度,根据中点得出AD的长度。连接BH,根据Rt△ADH的勾股定理求出DH的长度,从而得出△DGH的面积.
试题解析:(1)、∵∠ACB=90°,D是AB的中点,∴DC=DB=DA.∴∠B=∠DCB.又∵△ABC≌△FDE,
∴∠FDE=∠B.∴∠FDE=∠DCB.∴DG∥BC.∴∠AGD=∠ACB=90°.∴DG⊥AC.又∵DC=DA,
∴G是AC的中点.∴![]() .∴
.∴![]()
(2)、如图2所示:∵△ABC≌△FDE,∴∠B=∠1.∵∠C=90°,ED⊥AB,∴∠A+∠B=90°,∠A+∠2=90°,
∴∠B=∠2,∴∠1=∠2,∴GH=GD,∵∠A+∠2=90°,∠1+∠3=90°,∴∠A=∠3,∴AG=GD,
∴AG=GH,∴点G为AH的中点; 在Rt△ABC中,![]() ,
,
∵D是AB中点,∴![]() ,
,
连接BH.∵DH垂直平分AB,∴AB=BH.设AH=x,则BH=x,CH=8-x,
由勾股定理得:(8-x)2+62=x2,解得x=, ∴DH=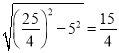 .
.
∴S△DGH=S△ADH=×××5=.
-
科目: 来源: 题型:
查看答案和解析>>【题目】分解因式:ax2﹣4a=
-
科目: 来源: 题型:
查看答案和解析>>【题目】某水果积极计划装运甲、乙、丙三种水果到外地销售(每辆汽车规定满载,并且只装一种水果).如表为装运甲、乙、丙三种水果的重量及利润.

(1)用8辆汽车装运乙、丙两种水果共22吨到A地销售,问装运乙、丙两种水果的汽车各多少辆?
(2)水果基地计划用20辆汽车装运甲、乙、丙三种水果共72吨到B地销售(每种水果不少于一车),假设装运甲水果的汽车为m辆,则装运乙、丙两种水果的汽车各多少辆?(结果用m表示)
(3)在(2)问的基础上,如何安排装运可使水果基地获得最大利润?最大利润是多少?
-
科目: 来源: 题型:
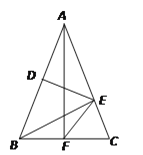
查看答案和解析>>【题目】如图,△ABC中,AB=AC,DE垂直平分AB,BE⊥AC,AF⊥BC,则∠EFC=____°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知正比例函数y=(4m+6)x , 当m 时,函数图象经过第二、四象限.
-
科目: 来源: 题型:
查看答案和解析>>【题目】请写出一个y随x增大而增大的正比例函数表达式,y=
-
科目: 来源: 题型:
查看答案和解析>>【题目】为了更好的保护美丽图画的邛海湿地,西昌市污水处理厂决定先购买A、B两型污水处理设备共20台,对邛海湿地周边污水进行处理,每台A型污水处理设备12万元,每台B型污水处理设备10万元.已知1台A型污水处理设备和2台B型污水处理设备每周可以处理污水640吨,2台A型污水处理设备和3台B型污水处理设备每周可以处理污水1080吨.
(1)求A、B两型污水处理设备每周分别可以处理污水多少吨?
(2)经预算,市污水处理厂购买设备的资金不超过230万元,每周处理污水的量不低于4500吨,请你列举出所有购买方案,并指出哪种方案所需资金最少?最少是多少?
相关试题

