【题目】如图,△ABC中,∠ACB=90°,AC=AN,BC=BM,则∠MCN=( )
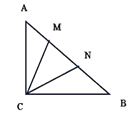
A. 30°B. 45°C. 60°D. 55°
参考答案:
【答案】B
【解析】
设∠BMC=x,∠ANC=y.由BC=BM,根据等边对等角得出∠BCM=∠BMC=x,利用三角形内角和定理得出∠B=180°-2x.同理得到∠ACN=∠ANC=y,∠A=180°-2y.根据直角三角形两锐角互余得出∠A+∠B=90°,那么x+y=135°,即∠BCM+∠ACN=135°,进而求出∠MCN=∠BCM+∠ACN-∠ACB=45°.
设∠BMC=x,∠ANC=y.
∵BC=BM,
∴∠BCM=∠BMC=x,∠B=180°-2x.
∵AC=AN,
∴∠ACN=∠ANC=y,∠A=180°-2y.
∵△ABC为直角三角形,∠ACB=90°,
∴∠A+∠B=90°,
∴180°-2y+180°-2x=90°,
∴x+y=135°,
∴∠BCM+∠ACN=135°,
∴∠MCN=∠BCM+∠ACN-∠ACB=135°-90°=45°.
故选B.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明做了一个数学实验:将一个圆柱形的空玻璃杯放入形状相同的无水鱼缸内,然后,小明对准玻璃杯口匀速注水,如图所示,在注水过程中,杯底始终紧贴鱼缸底部,则下面可以近似地刻画出无鱼水缸内最高水位
 与注水时间
与注水时间 之间的变化情况的是( )
之间的变化情况的是( )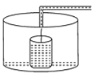
A.
 B.
B.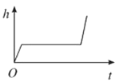
C.
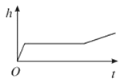 D.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,AB⊥AC,CD、BE分别是△ABC的角平分线,AG∥BC,AG⊥BG,下列结论:①∠BAG=2∠ABF;②BA平分∠CBG;③∠ABG=∠ACB;④∠CFB=135°,其中正确的结论有( )个

A.1B.2C.3D.4
-
科目: 来源: 题型:
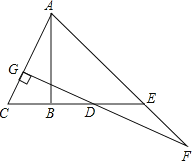
查看答案和解析>>【题目】如图,AB垂直平分线段CD(AB>CD),点E是线段CD延长线上的一点,且BE=AB,连接AC,过点D作DG⊥AC于点G,交AE的延长线与点F.
(1)若∠CAB=α,则∠AFG= (用α的代数式表示);
(2)线段AC与线段DF相等吗?为什么?
(3)若CD=6,求EF的长.
-
科目: 来源: 题型:
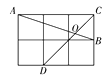
查看答案和解析>>【题目】如图,在边长为1的小正方形网格中,点A、B、C、D都在这些小正方形的顶点上,AB、CD相交于点O,则tan∠AOD=________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某段河流的两岸是平行的,数学兴趣小组在老师带领下不用涉水过河就测得的宽度,他们是这样做的:①在河流的一条岸边B点,选对岸正对的一棵树A;②沿河岸直走20m有一棵树C,继续前行20m到达D处;③从D处沿河岸垂直的方向行走,当到达A树正好被C树遮挡住的E处停止行走;④测得DE的长为5米.
(1)河的宽度是 米.
(2)请你说明他们做法的正确性.

-
科目: 来源: 题型:
查看答案和解析>>【题目】将下面的证明过程补充完整,括号内写上相应理由或依据:已知,如图,
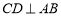 ,
, ,垂足分别为D、F,
,垂足分别为D、F,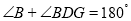 ,请试说明
,请试说明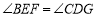 .
.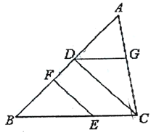
证明:∵
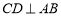 ,
, (已知)
(已知)∴
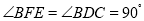 (____________________________)
(____________________________)∴
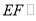 ________(____________________________)
________(____________________________)∴
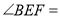 ________(____________________________)
________(____________________________)又∵
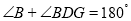 (已知)
(已知)∴
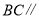 ________(____________________________)
________(____________________________)∴
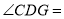 ________(____________________________)
________(____________________________)∴
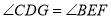 .
.
相关试题

