Question

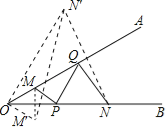
【题目】如图，∠AOB=30°，点M，N分别在边OA，OB上，OM=5，ON=12，点P，Q分别在边OB，OA上运动，连接MP，PQ，QN，则MP+PQ+QN的最小值为 ______ ．

Answer 1

【答案】13

【解析】试题分析：首先作M关于OB的对称点M′，作N关于OA的对称点N′，连接M′N′，即为MP+PQ+QN的最小值，易得△ONN′为等边三角形，△OMM′为等边三角形，∠N′OM′=90°，继而求得答案．

解：作M关于OB的对称点M′，作N关于OA的对称点N′，连接M′N′，即为MP+PQ+QN的最小值．

根据轴对称的定义可知：∠N′OQ=∠M′OB=30°，∠ONN′=60°，OM′=OM=5，ON′=ON=12，

∴△ONN′为等边三角形，△OMM′为等边三角形，

∴∠N′OM′=90°，

∴在Rt△M′ON′中，M′N′==13．

故答案为：13．