【题目】如图,抛物线y=ax2+bx+c(a≠0)的开口向上,与x轴交点的横坐标分别为﹣1、3,则下列说法错误的是( ) 
A.对称轴是直线x=1
B.方程ax2+bx+c=0的解是x1=﹣1,x2=3
C.当x<1,y随x的增大而增大
D.当﹣1<x<3时,y<0
参考答案:
【答案】C
【解析】解:∵抛物线与x轴交点的横坐标分别为﹣1、3, ∴对称轴是直线x= ![]() =1,方程ax2+bx+c=0的解是x1=﹣1,x2=3,故A、B正确;
=1,方程ax2+bx+c=0的解是x1=﹣1,x2=3,故A、B正确;
∵抛物线y=ax2+bx+c(a≠0)的开口向上,
∴当x<1,y随x的增大而减小,故C错误;
∵当﹣1<x<3时,抛物线在x轴的下面,
∴y<0,故D正确,
故选C.
【考点精析】解答此题的关键在于理解二次函数的性质的相关知识,掌握增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小,以及对抛物线与坐标轴的交点的理解,了解一元二次方程的解是其对应的二次函数的图像与x轴的交点坐标.因此一元二次方程中的b2-4ac,在二次函数中表示图像与x轴是否有交点.当b2-4ac>0时,图像与x轴有两个交点;当b2-4ac=0时,图像与x轴有一个交点;当b2-4ac<0时,图像与x轴没有交点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC,AC>BC.
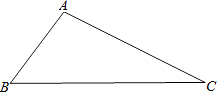
(1)尺规作图:在AC边上求作一点P,使PB=PC(保留作图痕迹,不写作法);
(2)若BC=6,∠C=30°,求△PBC的面积. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点E是△ABC的内心,AE的延长线和△ABC的外接圆相交于点D,连接BD、BE、CE,若∠CBD=32°,则∠BEC的度数为 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为9,将正方形折叠,使D点落在BC边上的点E处,折痕为GH.若BE:EC=2:1,则线段CH的长是 .

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A. =±2
=±2
B. =﹣16
=﹣16
C.x6÷x3=x2
D.(2x2)3=8x6 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD的边长为3cm,动点M从点B出发以3cm/s的速度沿着边BC﹣CD﹣DA运动,到达点A停止运动,另一动点N同时从点B出发,以1cm/s的速度沿着边BA向点A运动,到达点A停止运动,设点M运动时间为x(s),△AMN的面积为y(cm2),则y关于x的函数图象是( )
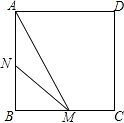
A.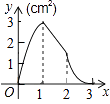
B.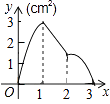
C.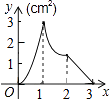
D.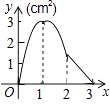
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在圆心角为90°的扇形OAB中,半径OA=4,C为
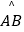 的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为 .
的中点,D、E分别为OA,OB的中点,则图中阴影部分的面积为 . 
相关试题

