【题目】(1)已知在△ABC中,∠A=90°,∠B=67.5°,请画一条直线,把这个三角形分割成两个等腰三角形(请你选用下面给出的备用图,把所有不同的分割方法都画出来.只需画图,不必说明理由,但要在图中标出相等两角的度数).
(2)已知在△ABC中,∠C是其最小的内角,过顶点B的一条直线把这个三角形分割成了两个等腰三角形,请探求∠ABC与∠C之间的关系.

参考答案:
【答案】(1)图形见解析(2) ∠ABC与∠C之间的关系是∠ABC=135°-![]() ∠C或∠ABC=3∠C或∠ABC=180°-3∠C或∠ABC=90°,∠C是小于45°的任意锐角.
∠C或∠ABC=3∠C或∠ABC=180°-3∠C或∠ABC=90°,∠C是小于45°的任意锐角.
【解析】试题分析:(1)已知角度,要分割成两个等腰三角形,可以运用直角三角形、等腰三角形性质结合三角形内角和定理,先计算出可能的角度,或者先从草图中确认可能的情况,及角度,然后画上.
(2)在(1)的基础上,由“特殊”到“一般”,需要把直角三角形分成两个等腰三角形的各种情形列方程,可得出角与角之间的关系.
试题解析:(1)如图①②(共有2种不同的分割法).

(2)设∠ABC=y,∠C=x,过点B的直线交边AC于点D.
在△DBC中,
①若∠C是顶角,如图,则∠CBD=∠CDB=90°-![]() x,∠A=180°-x-y.
x,∠A=180°-x-y.
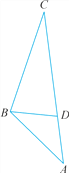
故∠ADB=180°-∠CDB=90°+![]() x>90°,此时只能有∠A=∠ABD,
x>90°,此时只能有∠A=∠ABD,
即180°-x-y=y-![]() ,
,
∴3x+4y=540°,∴∠ABC=135°-![]() ∠C.
∠C.
②若∠C是底角,
第一种情况:如图,当DB=DC时,∠DBC=x.在△ABD中,∠ADB=2x,∠ABD=y-x.

若AB=AD,则2x=y-x,此时有y=3x,
∴∠ABC=3∠C.
若AB=BD,则180°-x-y=2x,此时有3x+y=180°,∴∠ABC=180°-3∠C.
若AD=BD,则180°-x-y=y-x,此时有y=90°,即∠ABC=90°,∠C为小于45°的任意锐角.
第二种情况:如图,
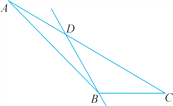
当BD=BC时,∠BDC=x,∠ADB=180°-x>90°,此时只能有AD=BD,∴∠A=∠ABD=![]() ∠BDC=
∠BDC=![]() ∠C<∠C,这与题设∠C是最小角矛盾.
∠C<∠C,这与题设∠C是最小角矛盾.
∴当∠C是底角时,BD=BC不成立.
综上所述,∠ABC与∠C之间的关系是∠ABC=135°-![]() ∠C或∠ABC=3∠C或∠ABC=180°-3∠C或∠ABC=90°,∠C是小于45°的任意锐角.
∠C或∠ABC=3∠C或∠ABC=180°-3∠C或∠ABC=90°,∠C是小于45°的任意锐角.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC内有一点D,且DA=DB=DC.若∠DAB=20°,∠DAC=30°,则∠BDC的度数为( )
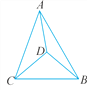
A. 100° B. 80° C. 70° D. 50°
-
科目: 来源: 题型:
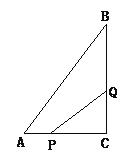
查看答案和解析>>【题目】如图4所示,在△ABC中,∠C=90°,AC=6cm,BC=8cm,点P从点A出发沿边AC向点C以1cm/s的速度移动,点Q从C点出发沿CB边向点B以2cm/s的速度移动.
(1)、如果P、Q同时出发,几秒钟后,可使△PCQ的面积为8平方厘米?
(2)、点P、Q在移动过程中,是否存在某一时刻,使得△PCQ的面积等于△ABC的面积的一半.若存在,求出运动的时间;若不存在,说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个等腰三角形两边长分别为5,6,则它的周长为( )
A. 16 B. 17 C. 16 或 17 D. 10 或 12
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图:已知在△ABC中,AB=AC,D为BC边的中点,过点D作DE⊥AB,DF⊥AC,,垂足分别为E,F.(1)、求证:△BED≌△CFD;(2)、若∠A=90°,求证:四边形DFAE是正方形.

-
科目: 来源: 题型:
查看答案和解析>>【题目】某单位在五月份准备组织部分员工到北京旅游,现联系了甲、乙两家旅行社,两家旅行社报价均为2000元/人,两家旅行社同时都对10人以上的团体推出了优惠举措:甲旅行社对每位员工七五折优惠;而乙旅行社是免去一位带队管理员工的费用,其余员工八折优惠.
【1】如果设参加旅游的员工共有a(a
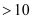 )人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含a的代数式表示,并化简.)
)人,则甲旅行社的费用为 元,乙旅行社的费用为 元;(用含a的代数式表示,并化简.)【2】假如这个单位现组织包括管理员工在内的共20名员工到北京旅游,该单位选择哪一家旅行社比较优惠?请说明理由.
【3】如果计划在五月份外出旅游连续七天,设最中间一天的日期为
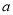 ,则这七天的日期之和为 .(用含
,则这七天的日期之和为 .(用含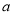 的代数式表示,并化简.)
的代数式表示,并化简.)【4】假如这七天的日期之和为63的倍数,则他们可能于五月几号出发?(写出所有符合条件的可能性,并写出简单的计算过程.)
-
科目: 来源: 题型:
查看答案和解析>>【题目】下图是由一些火柴棒搭成的图案:
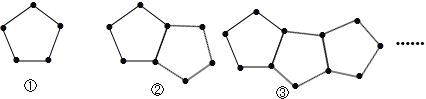
(1)摆第①个图案用 根火柴棒,摆第②个图案用 根火柴棒,摆第③个图案用 根火柴棒.
(2)按照这种方式摆下去,摆第n个图案用多少根火柴棒?
(3)计算一下摆121根火柴棒时,是第几个图案?
相关试题

