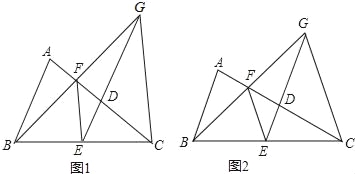
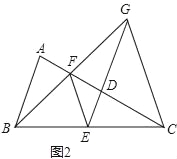
【题目】如图,已知等腰△ABC中,AC=BC,点D、E、F分别是线段AC、BC、AD的中点,连接FE、ED,BF的延长线交ED的延长线于点G,连接GC.
(1)求证:EF∥CG;
(2)若AC=![]() AB,求证:AC=CG;
AB,求证:AC=CG;
(3)如图2,若CG=EG,则![]() = .
= .
参考答案:
【答案】(1)证明见解析;
(2)证明见解析;
(3)![]()
【解析】
试题分析:(1)由点D、E分别是线段AC、BC的中点可得出DE为△ABC的中位线,根据中位线的性质即可得出∠CDE=∠A,进而可得出∠FDG=∠A,由此即可证出△ABF≌△DGF(ASA),根据全等三角形的性质即可得出BF=GF,即点F为线段BG的中点,再根据中位线的性质即可得出EF∥CG;
(2)过点C作CM⊥AB于点M,根据边与边的关系找出比例关系![]() =
=![]() =
=![]() ,由此即可得出△BAF∽△CAM,进而得出CF⊥BG,再由点F为线段BG的中点即可得出BC=CG,通过等量代换即可证出AC=CG;
,由此即可得出△BAF∽△CAM,进而得出CF⊥BG,再由点F为线段BG的中点即可得出BC=CG,通过等量代换即可证出AC=CG;
(3)根据DE∥AB即可得出∠GEC=∠CBA,结合两三角形为等腰三角形即可得出△GEC∽△CBA,再根据相似三角形的性质即可得出![]() ,代入数据即可得出结论.
,代入数据即可得出结论.
试题解析:(1)∵点D、E分别是线段AC、BC的中点,∴DE为△ABC的中位线,
∴DE∥AB,∴∠CDE=∠A.∵∠CDE=FDG,∴∠FDG=∠A.
∵点F为线段AD的中点,∴AF=DF.
在△ABF和△DGF中,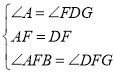 ,
,
∴△ABF≌△DGF(ASA),∴BF=GF,∴点F为线段BG的中点,
∵点E为线段BC的中点,∴EF为△BCG的中位线,∴EF∥CG.
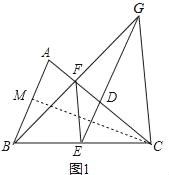
(2)在图1中,过点C作CM⊥AB于点M.∵AC=BC,
∴AM=BM=![]() AB.∵AC=
AB.∵AC=![]() AB,
AB,
∴![]() =
=![]() =
=![]() .∵AF=
.∵AF=![]() AD=
AD=![]() AC=
AC=![]() AB,∴
AB,∴![]() =
=![]() =
=![]() ,
,
∴△BAF∽△CAM,∴∠AFB=∠AMC=90°,∴CF⊥BG.
∵点F为线段BG的中点,∴BC=CG,又∵AC=BC,∴AC=CG.
(3)∵DE为△ABC的中位线,∴DE=![]() AB,CE=
AB,CE=![]() BC=
BC=![]() AC,∵DG=AB,EG=DE+DG,
AC,∵DG=AB,EG=DE+DG,
∴EG=![]() AB.∵DE∥AB,∴∠GEC=∠CBA,∵AC=BC,CG=EG,
AB.∵DE∥AB,∴∠GEC=∠CBA,∵AC=BC,CG=EG,
∴△GEC∽△CBA,∴![]() ,既
,既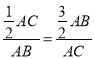 ,∴
,∴![]()
故答案为:![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:32°45′48″+21°25′14″.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形A1B1C1O,A2B2C2C1,A3B3C3C2,…按如图的方式放置.点A1,A2,A3,…和点C1,C2,C3,…分别在直线y=x+1和x轴上,则点B6的坐标是( )
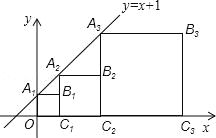
A.(63,32) B.(64,32) C.(63,31) D.(64,31)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,C为线段AE上一动点(不与点A,E重合),在AE同侧分别作等边△ABC和等边△CDE,AD与BE交于点O,AD与BC交于点P,BE与CD交于点Q,连接PQ.以下五个结论:
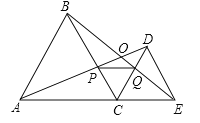
①AD=BE;②PQ∥AE;③AP=BQ;④DE=DP; ⑤∠AOB=60°.
其中正确的结论的个数是( )
A. 2个 B. 3个 C. 4个 D. 5个
-
科目: 来源: 题型:
查看答案和解析>>【题目】2020年4月24日,国家航天局在中国航天日线上启动仪式上公布:中国行星探测任务被命名为“天问系列”,首次火星探测任务被命名为“天问一号”.火星是与地球形貌最接近的大行星,火星也是我们的近邻,最近的时候距离地球约5500万千米.其中“5500万千米”用科学记数法表示为( )
A.550×108(米)B.55×109(米)
C.5.5×1010(米)D.0.55×1011(米)
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平面直角坐标系中,对于平面内任一点(m,n),规定以下两种变换: ⑴f(m,n)=(m,﹣n),如f(2,1)=(2,﹣1);
⑵g(m,n)=(﹣m,﹣n),如g (2,1)=(﹣2,﹣1)
按照以上变换有:f[g(3,4)]=f(﹣3,﹣4)=(﹣3,4),那么g[f(﹣3,2)]= . -
科目: 来源: 题型:
查看答案和解析>>【题目】我们把a、b两个数中较小的数记作min{a,b},直线y=kx﹣k﹣2(k<0)与函数y=min{x2﹣1、﹣x+1}的图象有且只有2个交点,则k的取值为 .
相关试题

