【题目】如图,已知△ABC中,∠ABC=90°,AB=BC,过△ABC的顶点B作直线![]() ,且点A到
,且点A到![]() 的距离为2,点C到
的距离为2,点C到![]() 的距离为3,则AC的长是( )
的距离为3,则AC的长是( )

A. ![]() B.
B. ![]() C.
C. ![]() D. 5
D. 5
参考答案:
【答案】C
【解析】
分别过A、C作AD⊥l于D,CE⊥l于E,根据锐角互余可得∠ABD=∠BCE,∠DAB=∠CBE,利用ASA可证明△ABD≌△CBE,即可得BD=CE,根据勾股定理可求出AB的长,再利用勾股定理求出AC的长即可.
分别过A、C作AD⊥l于D,CE⊥l于E,
∵点A到![]() 的距离为2,点C到
的距离为2,点C到![]() 的距离为3,
的距离为3,
∴AD=2,CE=3,
∵∠ABD+∠BAD=90°,∠ABD+∠CBE=90°,
∴∠BAD=∠CBE,
同理:∠ABD=∠BCE,
∵∠ABD=∠BCE,AB=BC,∠BAD=∠CBE,
∴△ABD≌△CBE,
∴BD=CE=3,
在Rt△ABD中,AB2=22+32=13,
在Rt△ABC中,AC2=AB2+BC2=13+13=26,
∴AC=![]() ,
,

故选C.
-
科目: 来源: 题型:
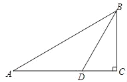
查看答案和解析>>【题目】如图,在△ABC中,∠C=90°,∠A=30°,BD是∠ABC的平分线,CD=5cm,求AB的长.
-
科目: 来源: 题型:
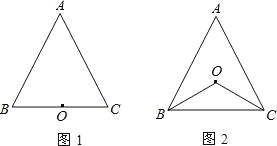
查看答案和解析>>【题目】已知,点O到△ABC的两边AB、AC所在直线的距离相等,且OB=OC.
(1)如图1,若点O在BC上,求证:△ABC是等腰三角形.
(2)如图2,若点O在△ABC内部,求证:AB=AC.
(3)若点O点在△ABC的外部,△ABC是等腰三角形还成立吗?请画图表示.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明同学在一次社会实践活动中,通过对某种蔬菜在1月份至7月份的市场行情进行统计分析后得出如下规律: ①该蔬菜的销售价P(单位:元/千克)与时间x(单位:月份)满足关系:P=9﹣x
②该蔬菜的平均成本y(单位:元/千克)与时间x(单位:月份)满足二次函数关系y=ax2+bx+10,已知4月份的平均成本为2元/千克,6月份的平均成本为1元/千克.
(1)求该二次函数的解析式;
(2)请运用小明统计的结论,求出该蔬菜在第几月份的平均利润L(单位:元/千克)最大?最大平均利润是多少?(注:平均利润=销售价﹣平均成本) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知∠A=∠AGE,∠D=∠DGC.
(1)试说明AB∥CD;
(2)若∠1+∠2=180°,且∠BEC=2∠B+60°,求∠C的度数.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB∥DC,AD∥BC,BE=DF,则图中全等的三角形有( )
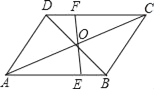
A. 3对 B. 4对 C. 5对 D. 6对
-
科目: 来源: 题型:
查看答案和解析>>【题目】将一副直角三角尺(即直角三角形AOB和直角三角形COD)的直角顶点O的重合,其中,在△AOB中,∠A=60°,∠B=30°,∠AOB=90°;在△COD中,∠C=∠D=45°,∠COD=90°.
(1)如图1,当OA在∠COD的外部,且∠AOC=45°时,①试说明CO平分∠AOB; ②试说明OA∥CD(要求书写过程);
(2)如图2,绕点O旋转直角三角尺AOB,使OA在∠COD的内部,且CD∥OB,试探索∠AOC=45°是否成立,并说明理由.

相关试题

