Question

【题目】如图，在平面直角坐标系中，正三角形OAB的顶点B的坐标为（2，0），点A在第一象限内，将△OAB沿直线OA的方向平移至△O′A′B′的位置，此时点A′的横坐标为3，则点B′的坐标为（ ）
A.（4，2 ）
B.（3，3 ）
C.（4，3 ）
D.（3，2 ）

Answer 1

【答案】A
【解析】解：如图，作AM⊥x轴于点M．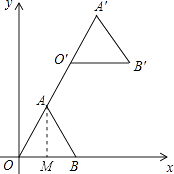
∵正三角形OAB的顶点B的坐标为（2，0），
∴OA=OB=2，∠AOB=60°，
∴OM= OA=1，AM= OM= ，
∴A（1， ），
∴直线OA的解析式为y= x，
∴当x=3时，y=3 ，
∴A′（3，3 ），
∴将点A向右平移2个单位，再向上平移2 个单位后可得A′，
∴将点B（2，0）向右平移2个单位，再向上平移2 个单位后可得B′，
∴点B′的坐标为（4，2 ），
故选A．
【考点精析】利用等边三角形的性质和坐标与图形变化-平移对题目进行判断即可得到答案，需要熟知等边三角形的三个角都相等并且每个角都是60°；新图形的每一点，都是由原图形中的某一点移动后得到的，这两个点是对应点；连接各组对应点的线段平行且相等．