【题目】定义:数学活动课上,乐老师给出如下定义:有一组对边相等而另一组对边不相等的凸四边形叫做对等四边形.
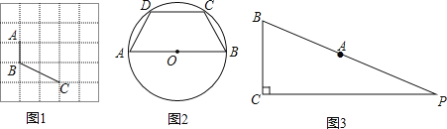
理解:(1)如图1,已知A、B、C在格点(小正方形的顶点)上,请在方格图中画出以格点为顶点,AB、BC为边的两个对等四边形ABCD;
(2)如图2,在圆内接四边形ABCD中,AB是⊙O的直径,AC=BD.求证:四边形ABCD是对等四边形;
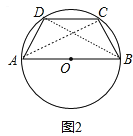
(3)如图3,在Rt△PBC中,∠PCB=90°,BC=11,tan∠PBC=![]() ,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
,点A在BP边上,且AB=13.用圆规在PC上找到符合条件的点D,使四边形ABCD为对等四边形,并求出CD的长.
参考答案:
【答案】(1)作图见解析;(2)证明见解析;(3)13、12-![]() 或12+
或12+![]() .
.
【解析】
试题分析:(1)根据对等四边形的定义,进行画图即可;
(2)连接AC,BD,证明Rt△ADB≌Rt△ACB,得到AD=BC,又AB是⊙O的直径,所以AB≠CD,即可解答;
(3)根据对等四边形的定义,分两种情况:①若CD=AB,此时点D在D1的位置,CD1=AB=13;②若AD=BC=11,此时点D在D2、D3的位置,AD2=AD3=BC=11;利用勾股定理和矩形的性质,求出相关相关线段的长度,即可解答.
试题解析:(1)如图1所示(画2个即可).
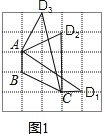
(2)如图2,连接AC,BD,
∵AB是⊙O的直径,
∴∠ADB=∠ACB=90°,
在Rt△ADB和Rt△ACB中,
![]()
∴Rt△ADB≌Rt△ACB,
∴AD=BC,
又∵AB是⊙O的直径,
∴AB≠CD,
∴四边形ABCD是对等四边形.
(3)如图3,点D的位置如图所示:
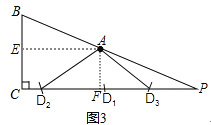
①若CD=AB,此时点D在D1的位置,CD1=AB=13;
②若AD=BC=11,此时点D在D2、D3的位置,AD2=AD3=BC=11,
过点A分别作AE⊥BC,AF⊥PC,垂足为E,F,
设BE=x,
∵tan∠PBC=![]() ,
,
∴AE=![]() x,
x,
在Rt△ABE中,AE2+BE2=AB2,
即x2+(![]() x)2=132,
x)2=132,
解得:x1=5,x2-5(舍去),
∴BE=5,AE=12,
∴CE=BC-BE=6,
由四边形AECF为矩形,可得AF=CE=6,CF=AE=12,
在Rt△AFD2中,FD2=![]() ,
,
∴CD2=CF-FD2=12-![]() ,CD3=CF+FD2=12+
,CD3=CF+FD2=12+![]() ,
,
综上所述,CD的长度为13、12-![]() 或12+
或12+![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】操场上有一根竖直立在地面上的旗杆,绳子自然下垂到地面还剩余2米,当把绳子拉开8米后,绳子刚好斜着拉直下端接触地面(如图①)
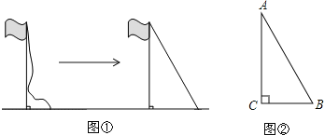
(1)请根据你的阅读理解,将题目的条件补充完整:如图②,Rt△ABC中 ∠C=90°,BC=8米,____________________________.求AC的长.
(2)根据(1)中的条件,求出旗杆的高度.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小明上午8点正从家里出发,到书店买书.右图反映了小明买书过程中(从出发到回家)离家的距离y(米)和离家的时间x(分)的关系.

(1)书店离小明家多远?
(2)若小明离开书店返回家时的平均速度比去书店时的平均速度每分钟快15米,问小明几点到家并求小明离开书店后返家过程中y与x的函数关系式.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在平行四边形ABCD中,E,F分别为边AB,CD的中点,连接DE,BF,BD.

(1)求证:△ADE≌△CBF.
(2)若AD⊥BD,则四边形BFDE是什么特殊四边形?请证明你的结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】在郴州市中小学“创园林城市,创卫生城市,创文明城市”演讲比赛中,5位评委给靓靓同学的评分如下:9.0,9.2,9.2,9.1,9.5,则这5个数据的平均数和众数分别是( )
A. 9.1,9.2 B. 9.2,9.2 C. 9.2,9.3 D. 9.3,9.2
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列计算正确的是( )
A. 2a3+3a3=5a6 B. (x5)3=x8
C. ﹣2m(m﹣3)=﹣2m2﹣6m D. (﹣3a﹣2)(﹣3a+2)=9a2﹣4
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形的周长为10cm,底边长为ycm,腰长为xcm,用x表示y的函数关系式为 ______ .
相关试题

