搜索
【题目】如图所示，A．B两地之间有一条河，原来从A地到B地需要经过桥DC，沿折线A→D→C→B到达B地，现在新建了桥EF，可直接沿直线AB从A地到达B地．BC=1000m，∠A=45°，∠B=37°．桥DC和AB平行，则现在从A地到达B地可比原来少走多少路程？（结果精确到1m．参考数据：
，sin37°≈0.60，cos37°≈0.80）
参考答案：
【答案】从A地到B地可比原来少走约446m.
【解析】分析：分别构造直角三角形将线段AD、DC、CB求出来，然后与线段AB的长相比较即能得到答案．
详解：如图,过点D作DH⊥AB于H,DG∥CB交AB于G.
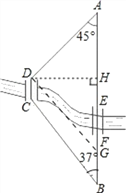
∵DC∥AB，
∴四边形DCBG为平行四边形。
∴DC=GB，GD=BC=1000.
∴两条路线路程之差为AD+DGAG.
在Rt△DGH中，
DH=DGsin37°≈1000×0.60=600m，
GH=DGcos37°≈1000×0.80≈800m.
在Rt△ADH中，
AD=
DH≈1.41×600≈846m.
AH=DH≈600m.
∴AD+DGAG=(846+1000)(600+800)≈446(m).
-
科目： 来源： 题型：
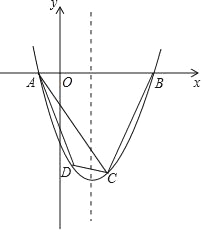
查看答案和解析>>【题目】如图，在平面直角坐标系中，已知抛物线y=x2+bx+c经过A、B、C三点，已知B（4，0），C（2，﹣6）．
（1）求该抛物线的解析式和点A的坐标；
（2）点D（m，n）（﹣1＜m＜2）在抛物线图象上，当△ACD的面积为
时，求点D的坐标；（3）在（2）的条件下，设抛物线的对称轴为l，点D关于l的对称点为E，能否在抛物线图象和l上分别找到点P、Q，使得以点D、E、P、Q为顶点的四边形为平行四边形？若能，求出点P的坐标；若不能，请说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】将图1中的正方形剪开得到图2，则图2中共有4个正方形；将图2中的一个正方形剪开得到图3，图3中共有7个正方形；将图3中4个较小的正方中的一个剪开得到图4，则图4中共有10个正方形，照这个规律剪下去……
（1）根据图中的规律补全下表：
图形标号
1
2
3
4
5
6
n
正方形个数
1
4
7
10
（2）求第几幅图形中有2020个正方形？
-
科目： 来源： 题型：
查看答案和解析>>【题目】根据给出的数轴及已知条件，解答下面的问题：
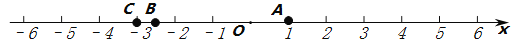
（1）已知点A，B，C表示的数分别为1，
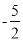，-3.观察数轴，与点A的距离为3的点表示的数是 ，A，B两点之间的距离为 。（2）数轴上，点B关于点A的对称点表示的数是 ；
（3）若将数轴折叠，使得A点与C点重合，则与B点重合的点表示的数是 ；若此数轴上M，N两点之间的距离为2019（M在N的左侧），且当A点与C点重合时，M点与N点也恰好重合，则点M表示的数是 ，点N表示的数是 。
（4）若数轴上P，Q两点间的距离为a（P在Q的左侧），表示数b的点到P，Q的两点的距离相等，将数轴折叠，当P点与Q点重合时，点P表示的数是 ，点Q表示的数是 （用含a，b的式子表示这两个数）。
-
科目： 来源： 题型：
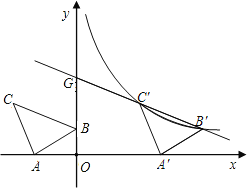
查看答案和解析>>【题目】如图，在平面直角坐标系中有Rt△ABC，∠A＝90°，AB＝AC，A（－2，0）、
B（0，1）、C（d，2）。
（1）求d的值；
（2）将△ABC沿x轴的正方向平移，在第一象限内B、C两点的对应点B′、C′正好落在某反比例函数图
像上。请求出这个反比例函数和此时的直线B′C′的解析式；
（3）在（2）的条件下，直线B′C′交y轴于点G。问是否存在x轴上的点M和反比例函数图像上的点P，
使得四边形PGMC′是平行四边形。如果存在，请求出点M和点P的坐标；如果不存在，请说明理由。
-
科目： 来源： 题型：
查看答案和解析>>【题目】某学校开展课外体育活动，决定开展：篮球、乒乓球、踢毽子、跑步四种活动项目.为了解学生最喜欢哪一种活动项目（每人只选取一种）.随机抽取了部分学生进行调查，并将调查结果绘成如下统计图，请你结合图中信息解答下列问题.
（1）样本中最喜欢篮球项目的人数所占的百分比为 ，其所在扇形统计图中对应的圆心角度数是 度；
（2）请把条形统计图补充完整；
（3）若该校有学生1000人，请根据样本估计全校最喜欢踢毽子的学生人数约是多少？
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图所示，正方形网格中，△ABC为格点三角形（即三角形的顶点都在格点上）．
（1）把△ABC沿BA方向平移后，点A移到点A1，在网格中画出平移后得到的△A1B1C1；
（2）把△A1B1C1绕点A1按逆时针方向旋转90°，在网格中画出旋转后的△A1B2C2；
（3）如果网格中小正方形的边长为1，求点B经过（1）、（2）变换的路径总长．
相关试题
