【题目】如图,抛物线的顶点为C(1,﹣2),直线y=kx+m与抛物线交于A、B来两点,其中A点在x轴的正半轴上,且OA=3,B点在y轴上,点P为线段AB上的一个动点(点P与点A、B不重合),过点P且垂直于x轴的直线与这条抛物线交于点E.
(1)求直线AB的解析式.
(2)设点P的横坐标为x,求点E的坐标(用含x的代数式表示).
(3)求△ABE面积的最大值.

参考答案:
【答案】(1)直线AB解析式为y=![]() x﹣
x﹣![]() ;
;
(2)E点的坐标为(x, ![]() x2﹣x﹣
x2﹣x﹣![]() );
);
(3)△ABE面积的最大值为![]() .
.
【解析】试题分析:(1)由条件可先求得抛物线解析式,则可求得B点坐标,再利用待定系数法可求得直线AB解析式;
(2)由条件可知P、E的横坐标相同,又点E在抛物线上,则可表示出E点坐标;
(3)由(2)可用x表示出PE的长,则可用x表示出△ABE的面积,再利用二次函数的性质可求得其最大值.
试题解析:(1)∵抛物线顶点坐标为(1,﹣2),
∴可设抛物线解析式为y=a(x﹣1)2﹣2,
∵OA=3,且点A在x轴的正半轴上,
∴A(3,0),
∴0=a(3﹣1)2﹣2,解得a=![]() ,
,
∴抛物线解析式为y=![]() (x﹣1)2﹣2=
(x﹣1)2﹣2=![]() x2﹣x﹣
x2﹣x﹣![]() ,当x=0时可得y=﹣
,当x=0时可得y=﹣![]() ,
,
∴B(0,﹣![]() ),
),
设直线AB解析式为y=kx+b,把A、B坐标代入可得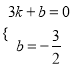 ,解得
,解得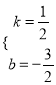 ,
,
∴y=![]() x﹣
x﹣![]() ;
;
(2)∵点P为线段AB上的一个动点,且PE⊥x轴,
∴点E的横坐标为x,
∵点E在抛物线上,
∴E点的坐标为(x, ![]() x2﹣x﹣
x2﹣x﹣![]() );
);
(3)∵点P为线段AB上的一点,
∴P(x, ![]() x﹣
x﹣![]() ),则E(x,
),则E(x, ![]() x2﹣x﹣
x2﹣x﹣![]() ),
),
∴PE=![]() x﹣
x﹣![]() ﹣(
﹣(![]() x2﹣x﹣
x2﹣x﹣![]() )=﹣
)=﹣![]() x2+
x2+![]() x,
x,
由(2)可知点B到PE的距离x,点A以PE的距离为3﹣x,
∴S△ABE=![]() PEx+
PEx+![]() PE(3﹣x)=
PE(3﹣x)=![]() PE(x+3﹣x)=
PE(x+3﹣x)=![]() PE=
PE=![]() (﹣
(﹣![]() x2+
x2+![]() x)=﹣
x)=﹣![]() x2+
x2+![]() x=﹣
x=﹣![]() (x﹣
(x﹣![]() )2+
)2+![]() ,
,
∵﹣![]() <0,
<0,
∴当x=![]() 时,S△ABE有最大值,最大值为
时,S△ABE有最大值,最大值为![]() ,
,
∴△ABE面积的最大值为![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,已知△ABC的三个顶点的坐标分别为A(﹣3,5),B(﹣2,1),C(﹣1,3).
(1)若△ABC经过平移后得到△A1B1C1,已知点C1的坐标为(4,0),写出顶点A1,B1的坐标,并画出△A1B1C1;
(2)若△ABC和△A2B2C2关于原点O成中心对称图形,写出△A2B2C2的各顶点的坐标;
(3)将△ABC绕着点O按顺时针方向旋转90°得到△A3B3C3,写出△A3B3C3的各顶点的坐标,并画出△A3B3C3.

-
科目: 来源: 题型:
查看答案和解析>>【题目】“x的3倍与y的和不小于2”用不等式可表示为( )
A. 3x+y>2 B. 3(x+y)>2 C. 3x+y≥2 D. 3(x+y)≥2
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在AC⊥BC,过点C的直线MN∥AB,D为AB边上一点,且AD=4,过点D作DE⊥BC,交直线MN于E,垂足为F,连接CD、BE.
(1)求CE的长;
(2)当D在AB中点时,四边形BECD是什么特殊四边形?说明你的理由;

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一次函数y1=2x-6,y2=-5x+1,则当x________时,y1>y2.
-
科目: 来源: 题型:
查看答案和解析>>【题目】把x2﹣4x+1化为(x+h)2+k(其中h、k是常数)的形式是__________ .
-
科目: 来源: 题型:
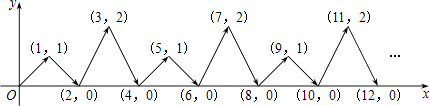
查看答案和解析>>【题目】如图,动点P在平面直角坐标系中按图中箭头所示的方向运动,第1次从原点运动到(1,1),第2次接着运动到点(2,0),第3次接着运动到点(3,2),…,按这样的运动规律,经过2017次运动后,动点P的坐标为 .
相关试题

