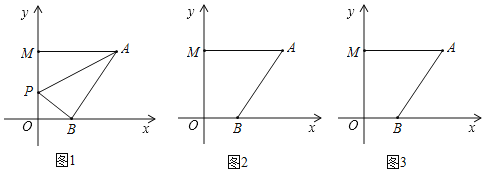
【题目】在平面直角坐标系中,A(6,a),B(b,0),M(0,c),P点为y轴上一动点,且(b﹣2)2+|a﹣6|+![]() =0.
=0.
(1)求点B、M的坐标;
(2)当P点在线段OM上运动时,试问是否存在一个点P使S△PAB=13,若存在,请求出P点的坐标与AB的长度;若不存在,请说明理由.
(3)不论P点运动到直线OM上的任何位置(不包括点O、M),∠PAM、∠APB、∠PBO三者之间是否都存在某种固定的数量关系,如果有,请利用所学知识找出并证明;如果没有,请说明理由.
参考答案:
【答案】(1)M(0,6),B(2,0),A(6,6);(2)AB=2![]() ;(3)①当点P在线段OM上时,结论:∠APB+∠PBO=∠PAM;理由见解析;②当点P在MO的延长线上时,结论:∠APB+∠PBO=∠PAM.理由见解析;③当点P在OM的延长线上时,结论:∠PBO=∠PAM+∠APB.理由见解析;
;(3)①当点P在线段OM上时,结论:∠APB+∠PBO=∠PAM;理由见解析;②当点P在MO的延长线上时,结论:∠APB+∠PBO=∠PAM.理由见解析;③当点P在OM的延长线上时,结论:∠PBO=∠PAM+∠APB.理由见解析;
【解析】
(1)利用非负数的性质,求出a、b、c即可解决问题;
(2)设P(0,m).根据S△PAB=S梯形AMOB-S△APM-S△PBO,构建方程即可解决问题;
(3)分三种情形,分别画出图形解决问题即可.
(1)∵(b-2)2+|a-6|+![]() =0,
=0,
又∵(b-2)2,≥0,|a-6|≥0,![]() ≥0,
≥0,
∴a=6,b=2,c=6.
∴M(0,6),B(2,0),A(6,6),
(2)设P(0,m).
∵S△PAB=13,四边形AMOB是直角梯形,
∴![]() (6+2)6-
(6+2)6-![]() m2-
m2-![]() (6-m)6=13,
(6-m)6=13,
∴m=![]() ,
,
∴P(0,![]() ),
),
AB=![]() =2
=2![]() .
.
(3)①如图2-1中,当点P在线段OM上时,结论:∠APB+∠PBO=∠PAM;
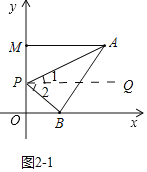
理由:作PQ∥AM,则PQ∥AM∥ON,
∴∠1=∠PAM,∠2=∠PBO,
∴∠1+∠2=∠PAM+∠PBO,
即∠APB=∠PAM+∠PBO,
∠APB+∠PBO=∠PAM;
②如图2-2中所示,当点P在MO的延长线上时,结论:∠APB+∠PBO=∠PAM.
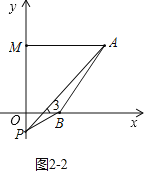
理由:∵AM∥OB,
∴∠PAM=∠3,
∵∠3=∠APB+∠PBO,
∴∠APB+∠PBO=∠PAM.
③如图2-3中,当点P在OM的延长线上时,结论:∠PBO=∠PAM+∠APB.
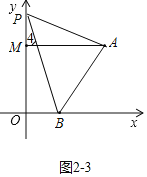
理由:∵AM∥OB,
∴∠4=∠PBO,
∵∠4=∠PAM+∠APB,
∴∠PBO=∠PAM+∠APB.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读下列一段文字,再回答问题:
已知平面内两点P1(x1,y1)、P2(x2,y2),这两点间的距离P1P2=
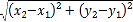 .同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.
.同时当两点所在的直线在坐标轴上或平行于坐标轴或垂直于坐标轴时,两点间的距离公式可简化为|x2﹣x1|或|y2﹣y1|.(1)已知点A(2,3)、B(4,2),试求A、B两点间的距离;
(2)已知点A、B在平行于x轴的直线上,点A的横坐标为7,点B的横坐标为5,试求A、B两点间的距离;
(3)已知一个三角形的各顶点坐标为A(﹣2,1)、B(1,4)、C(1﹣a,5),试用含a的式子表示△ABC的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,随着我市铁路建设进程的加快,现规划从A地到B地有一条笔直的铁路通过,但在附近的C处有一大型油库,现测得油库C在A地的北偏东60°方向上,在B地的西北方向上,AB的距离为250(
 +1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.
+1)米.已知在以油库C为中心,半径为200米的范围内施工均会对油库的安全造成影响.问若在此路段修建铁路,油库C是否会受到影响?请说明理由.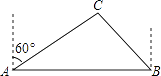
-
科目: 来源: 题型:
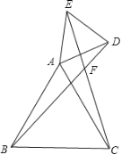
查看答案和解析>>【题目】如图,已知△ABC和△ADE均为等边三角形,BD、CE交于点F.
(1)求证:BD=CE;(2)求锐角∠BFC的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】先阅读,再解题
解方程(x﹣1)2﹣5(x﹣1)+4=0,可以将(x﹣1)看成一个整体,设x﹣1=y,则原方程可化y2﹣5y+4=0,解得y1=1;y2=4,当y=1时,即x﹣1=1,解得x=2,当y=4时,即x﹣1=4,解得x=5,所 原方程的解为x1=2,x2=5
请利用上述这种方法解方程:(3x﹣5)2﹣4(5﹣3x)+3=0.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,直线MN与直线AB、CD分别交于点E、F,∠1与∠2互补.
(1)试判断直线AB与直线CD的位置关系,并说明理由;
(2)如图2,∠BEF与∠EFD的角平分线交于点P,EP与CD交于点G,点H是MN上一点,且GH⊥EG,求证:PF∥GH;
(3)如图3,在(2)的条件下,连接PH,K是GH上一点使∠PHK=∠HPK,作PQ平分∠EPK,问∠HPQ的大小是否发生变化?若不变,请求出其值;若变化,说明理由.

-
科目: 来源: 题型:
查看答案和解析>>【题目】两块等腰直角三角形纸片AOB和COD按图1所示放置,直角顶点重合在点O处,AB=25,CD=17.保持纸片AOB不动,将纸片COD绕点O逆时针旋转α(0°<α<90°)角度,如图2所示.
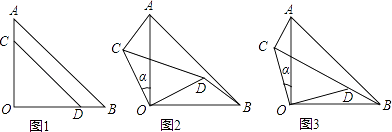
(1)利用图2证明AC=BD且AC⊥BD;
(2)当BD与CD在同一直线上(如图3)时,求AC的长和α的正弦值.
相关试题

