【题目】2019年暑假期间,某学校计划租用8辆客车送280名师生参加社会实践活动,现有甲、乙两种客车,它们的载客量和租金如表,设租用甲种客车x辆,租车总费用为w元.
甲种客车 | 乙种客车 | |
载客量(人/辆) | 30 | 40 |
租金(元/辆) | 270 | 320 |
(1)求出w(元)与x(辆)之间函数关系式,并直接写出自变量x的取值范围;
(2)选择怎样的租车方案所需的费用最低?最低费用多少元?
参考答案:
【答案】(1)![]() (
(![]() 且x为整数);(2)租用甲种客车4辆,租用乙种客车4辆,所需的费用最低,为2360元.
且x为整数);(2)租用甲种客车4辆,租用乙种客车4辆,所需的费用最低,为2360元.
【解析】
(1)根据题意租金×客车数量=租车总费用列出方程即可,根据车辆不能超过计划数量8且要满足载客总数大于等于280人列出不等式求解即可;
(2)根据(1)中得出的表达式判断w随x的增大而减小,再根据自变量x的取值范围取最大值求解即可.
解:(1)设租用甲种客车x辆,则租用乙种客车![]() 辆,
辆,
由题意可得出![]()
由题意可知: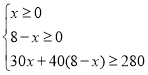
解得![]() 且x为整数
且x为整数
∴自变量x的取值范围为:![]() 且x为整数;
且x为整数;
(2)∵![]() 中x的系数
中x的系数![]() ,
,
∴w随x的增大而减小,
∴当x取最大值时即![]() 时,w的值最小,
时,w的值最小,
其最小值为![]() 元,
元,
∴租用甲种客车4辆,租用乙种客车4辆,所需的费用最低,为2360元.
-
科目: 来源: 题型:
查看答案和解析>>【题目】广宇同学以每千克1.1元的价格从批发市场购进若干千克西瓜到周谷堆市场上销售,在销售了40千克之后,余下的打七五折全部售完.销售金额y(元)与售出西瓜的千克数x(千克)之间的关系如图所示.下列结论正确的是( )

A.降价后西瓜的单价为2元/千克B.广宇一共进了50千克西瓜
C.售完西瓜后广宇获得的总利润为44元D.降价前的单价比降价后的单价多0.6元
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知AB为⊙O的直径,BD和CD为⊙O的切线,切点分别为B和C.
(1)求证:AC∥OD;
(2)当BC=BD,且BD=6cm时,求图中阴影部分的面积(结果不取近似值).

-
科目: 来源: 题型:
查看答案和解析>>【题目】在水果销售旺季,某水果店购进一优质水果,进价为 20 元/千克,售价不低于 20 元/千克,且不超过 32 元/千克,根据销售情况,发现该水果一天的销售量 y(千克)与该天的售价 x(元/千克)满足如下表所示的一次函数关系.
销售量 y(千克)
…
34.8
32
29.6
28
…
售价 x(元/千克)
…
22.6
24
25.2
26
…
(1)某天这种水果的售价为 23.5 元/千克,求当天该水果的销售量.
(2)如果某天销售这种水果获利 150 元,那么该天水果的售价为多少元?
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,一只蚂蚁在网格(每小格边长为1)上沿着网格线运动.它从格点
 处出发去看望格点B、C、D等处的蚂蚁,规定:向上向右走均为正,向下向左走均为负.如:从A到B记为:
处出发去看望格点B、C、D等处的蚂蚁,规定:向上向右走均为正,向下向左走均为负.如:从A到B记为: ,从B到A记为:
,从B到A记为: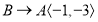 ,其中第一个数表示左右方向,第二个数表示上下方向.
,其中第一个数表示左右方向,第二个数表示上下方向.
(1)填空:图中
 ,
, ;
;(2)若这只蚂蚁从A处去M处的蚂蚁的行走路线依次为
 ,
, ,
, ,
, ,则点M的坐标为(________,________);
,则点M的坐标为(________,________);(3)若图中另有两个格点Р、Q,且
 ,
, ,则从Q到A记为________________.
,则从Q到A记为________________. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两人驾车都从Р地出发,沿一条笔直的公路匀速前往Q地,乙先出发一段时间后甲再出发,甲、乙两人到达Q地后均停止,已知P、Q两地相距200 km,设乙行驶的时间为t(h),甲、乙两人之间的距离为y(km),表示y与t函数关系的部分图象如图所示.请解决以下问题:

(1)由图象可知,甲比乙迟出发________h.图中线段BC所在直线的函数解析式为________________;
(2)设甲的速度为
 ,求出
,求出 的值;
的值;(3)根据题目信息补全函数图象(不需要写出分析过程,但必须标明关键点的坐标);并直接写出当甲、乙两人相距32 km时t的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在Rt△ABC中,∠A=90°,AB=AC,点D,E分别在边AB,AC上,AD=AE,连接DC,点M,P,N分别为DE,DC,BC的中点.
(1)观察猜想
图1中,线段PM与PN的数量关系是 ,位置关系是 ;
(2)探究证明
把△ADE绕点A逆时针方向旋转到图2的位置,连接MN,BD,CE,判断△PMN的形状,并说明理由;
(3)拓展延伸
把△ADE绕点A在平面内自由旋转,若AD=4,AB=10,请直接写出△PMN面积的最大值.

相关试题

