【题目】如图,在边长为2 ![]() 的正方形ABCD中,点E为AD边的中点,将△ABE沿BE翻折,使点A落在点A′处,作射线EA′,交BC的延长线于点F,则CF= .
的正方形ABCD中,点E为AD边的中点,将△ABE沿BE翻折,使点A落在点A′处,作射线EA′,交BC的延长线于点F,则CF= . 
参考答案:
【答案】![]()
【解析】解:∵正方形ABCD,
∴AB=AD=BC=2 ![]() ,AD∥BC,
,AD∥BC,
∴∠AEB=∠EBF,
∵E为AD边的中点,
∴AE= ![]() ,
,
由折叠的性质得∠AEB=∠BEF,EA′=AE= ![]() ,∠BA′E=∠A=90°,A′B=AB=2
,∠BA′E=∠A=90°,A′B=AB=2 ![]() ,
,
∴∠BEF=∠EBF,
∴BF=EF,
设CF=x,则BF=2 ![]() +x,A′F=
+x,A′F= ![]() +x,
+x,
在Rt△A′BF中,(2 ![]() )2+(
)2+( ![]() +x)2=(2
+x)2=(2 ![]() +x)2 ,
+x)2 ,
解得:x= ![]() ,
,
所以答案是 ![]() .
.
【考点精析】关于本题考查的翻折变换(折叠问题),需要了解折叠是一种对称变换,它属于轴对称,对称轴是对应点的连线的垂直平分线,折叠前后图形的形状和大小不变,位置变化,对应边和角相等才能得出正确答案.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知关于x的分式方程

(1)若方程的增根为x=1,求m的值
(2)若方程有增根,求m的值
(3)若方程无解,求m的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,点O是直线AB上任一点,射线OD和射线OE分别平分∠AOC和∠BOC.

(1)填空:与∠AOE互补的角是 ;
(2)若∠AOD=36°,求∠DOE的度数;
(3)当∠AOD=x°时,请直接写出∠DOE的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知△ABC中,
 厘米,
厘米,  厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______ 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
厘米,点D为AB的中点.如果点P在线段BC上以4厘米/秒的速度由B点向C点运动,同时,点Q在线段CA上由C点向A点运动.当点Q的运动速度为_______ 厘米/秒时,能够在某一时刻使△BPD与△CQP全等.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,△ABC的三个顶点分别为A(2,3),B(3,1),C(-2,-2).
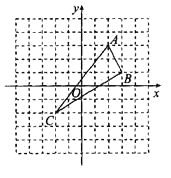
(1)请在图中作出△ABC关于y轴的轴对称图形△A′B′C′(A,B,C的对称点分别是A′,B′,C′),并直接写出A′,B′,C′的坐标.
(2)求△A′B′C′的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某同学报名参加学校秋季运动会,有以下5个项目可供选择:径赛项目:100m、200m、1000m(分别用A1、A2、A3表示);田赛项目:跳远,跳高(分别用T1、T2表示).
(1)该同学从5个项目中任选一个,恰好是田赛项目的概率P为;
(2)该同学从5个项目中任选两个,求恰好是一个径赛项目和一个田赛项目的概率P1 , 利用列表法或树状图加以说明;
(3)该同学从5个项目中任选两个,则两个项目都是径赛项目的概率P2为 . -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在矩形ABCD中,对角线AC与BD相交于点O,过点A作AE∥BD,过点D作ED∥AC,两线相交于点E.

(1)求证:四边形AODE是菱形;
(2)连接BE,交AC于点F.若BE⊥ED于点E,求∠AOD的度数.
相关试题

