【题目】定义：如图1，对于直线同侧的、两点，若在上的点满足，则称为、两点在上的反射点，与的和称为、两点的反射距离．

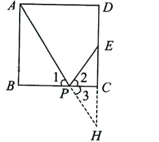
（1）如图2，在边长为2的正方形中，为的中点，为、两点在直线上的反射点，求、两点的反射距离；

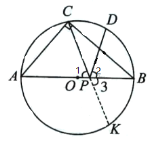
（2）如图3，内接于，直径为4，，点为劣弧上一动点，点为、两点在上的反射点，当、两点的反射距离最大时，求劣弧的长；

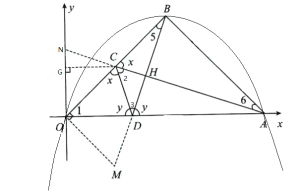
（3）如图4，在平面直角坐标系中，抛物线与轴正半轴交于点，顶点为，若点为点、在上的反射点，同时点为点、在上的反射点．

①请判断线段和的位置关系，并给出证明；

②求、两点的反射距离与、两点的反射距离的比值．

【答案】（1）；（2）；（3）①，证明见解析；②

【解析】

（1）延长交的延长线于点，根据题意得出，结合公共边和直角相等证明，然后进一步根据勾股定理求解即可；

（2）作点关于的对称点，由此得出，进一步证明、、三点共线，然后利用当经过圆心时，反射距离最大进一步求解即可；

（3）①根据题意得出点A、B的坐标，延长交轴于点，作交延长线于点，根据三角形内角和定理进一步求出∠CHD是直角，由此证明结论即可；②根据题意先后证明、，利用全等三角形性质得出点C是OB中点，根据勾股定理求出BM，然后过C点作于点G，进一步通过证明得出，利用相似三角形性质求出ON，再根据勾股定理求出AN，据此进一步求解即可.

（1）如图，延长交的延长线于点，

∵，，

∴，

又∵，，

∴，

∴，，

∴；

（2）如图，作点关于的对称点，

则，

∴ ，

又∵，，

∴，

∴、、三点共线，

∴当经过圆心时，反射距离最大．

此时点与点重合，求得：，

∴劣弧；

（3）①如图延长交轴于点，作交延长线于点，

由题可得：，，

∴∠1=45°，

设∠ACB=∠DCO=，∠CDO=∠BDA=，

∵，∠1=45°，

∴，，，

∴，

∴；

②∵，

∴，

∵点B为抛物线顶点，

∴B点在OA的垂直平分线上，

∴OB=AB，

∵∠1=45°，

∴∠ABC=90°，

在△BOM与△ABC中，

∵，OB=BA，∠BOM=∠CBA，

∴△BOM△ABC，

∴，

∵∠1=45°，

∴∠MOD=∠1=45°，

∵∠MDO=∠BDA，∠BDA=∠CDO，

∴∠MDO=∠CDO，

在△CDO与△MDO中，

∵∠1=∠MOD，OD=OD，∠MDO=∠CDO，

∴△CDO△MDO，

∴，

则为的中点，，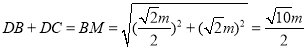

过C点作于点G，则，，

∵，

∴CG∥OA，

∴△NGC~△NOA，

∴，

∴，

∴，

∴.

关闭