【题目】已知二次函数y=ax2+bx+c(a≠0)的图象如图所示,有下列4个结论:①abc>0;②b<a+c;③4a+2b+c>0;④b2﹣4ac>0;其中正确的结论有( )
A.1个
B.2个
C.3个
D.4个
参考答案:
【答案】B
【解析】解:①∵抛物线开口向下,
∴a<0.
∵抛物线的对称轴为x=﹣ ![]() =1,
=1,
∴b=﹣2a>0.
当x=0时,y=c>0,
∴abc<0,①错误;
②当x=﹣1时,y<0,
∴a﹣b+c<0,
∴b>a+c,②错误;
③∵抛物线的对称轴为x=1,
∴当x=2时与x=0时,y值相等,
∵当x=0时,y=c>0,
∴4a+2b+c=c>0,③正确;
④∵抛物线与x轴有两个不相同的交点,
∴一元二次方程ax2+bx+c=0,
∴△=b2﹣4ac>0,④正确.
综上可知:成立的结论有2个.
故选B.
由抛物线的开口方程、抛物线的对称轴以及当x=0时的y值,即可得出a、b、c的正负,进而即可得出①错误;由x=﹣1时,y<0,即可得出a﹣b+c<0,进而即可得出②错误;由抛物线的对称轴为x=1结合x=0时y>0,即可得出当x=2时y>0,进而得出4a+2b+c=c>0,③成立;由二次函数图象与x轴交于不同的两点,结合根的判别式即可得出△=b2﹣4ac>0,④成立.综上即可得出结论.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,二次函数y=(x+2)2+m的图象与y轴交于点C,点B在抛物线上,且与点C关于抛物线的对称轴对称,已知一次函数y=kx+b的图象经过该二次函数图象上的点A(﹣1,0)及点B.

(1)求二次函数与一次函数的解析式;
(2)根据图象,写出满足(x+2)2+m≥kx+b的x的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两名大学生去距学校36千米的某乡镇进行社会调查.他们从学校出发,骑电动车行驶20分钟时发现忘带相机,甲下车前往,乙骑电动车按原路返回.乙取相机后(在学校取相机所用时间忽略不计),骑电动车追甲.在距乡镇13.5千米处追上甲后同车前往乡镇.乙电动车的速度始终不变.设甲与学校相距y甲(千米),乙与学校相离y乙(千米),甲离开学校的时间为t(分钟).y甲、y乙与x之间的函数图象如图所示,结合图象解答下列问题:
(1)电动车的速度为 千米/分钟;
(2)甲步行所用的时间为 分;
(3)求乙返回到学校时,甲与学校相距多远?
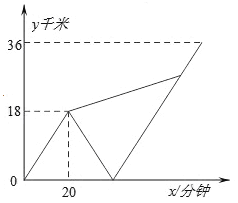
-
科目: 来源: 题型:
查看答案和解析>>【题目】在同一直角坐标系中,函数y=mx+m和y=﹣mx2+2x+2(m是常数,且m≠0)的图象可能是( )
A.
B.
C.
D.
-
科目: 来源: 题型:
查看答案和解析>>【题目】一辆旅游车从大理返回昆明,旅游车到昆明的距离y(km)与行驶时间x(h)之间的函数关系如图所示,试回答下列问题:
(1)求距离y(km)与行驶时间x(h)的函数表达式(不求自变量的取值范围);
(2)若旅游车8:00从大理出发,11:30在某加油站加油,问此时旅游车距离昆明还有多远(途中停车时间不计)?

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,正方形ABCD边长为2,E为CD的中点,以点A为中心,把△ADE顺时针旋转90°得△ABF,连接EF,则EF的长等于 .
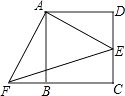
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图①,在△AOB中,∠AOB=90°,OA=3,OB=4.将△AOB沿x轴依次以点A、B、O为旋转中心顺时针旋转,分别得到图②、图③、…,则旋转得到的图⑩的直角顶点的坐标为
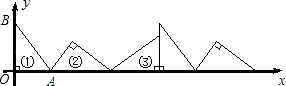
相关试题

