【题目】如图,平面直角坐标系中,矩形![]() 的对角线
的对角线![]() ,
,![]() .
.
(1)求点![]() 的坐标;
的坐标;
(2)把矩形![]() 沿直线
沿直线![]() 对折,使点
对折,使点![]() 落在点
落在点![]() 处,折痕
处,折痕![]() 分别与
分别与![]() 、
、![]() 、
、![]() 相交于点
相交于点![]() 、
、![]() 、
、![]() ,求直线
,求直线![]() 的解析式;
的解析式;
(3)若点![]() 在直线
在直线![]() 上,平面内是否存在点
上,平面内是否存在点![]() ,使以
,使以![]() 、
、![]() 、
、![]() 、
、![]() 为顶点的四边形是菱形?若存在,请直接写出点
为顶点的四边形是菱形?若存在,请直接写出点![]() 的坐标;若不存在,请说明理由.
的坐标;若不存在,请说明理由.

参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ;(3)存在符合条件的点
;(3)存在符合条件的点![]() 共有4个,分别为
共有4个,分别为 ![]()
![]()
![]()
![]()
【解析】
(1)利用三角函数求得OA以及OC的长度,则B的坐标即可得到;
(2)分别求出D点和E点坐标,即可求得DE的解析式;
(3)分当FM是菱形的边和当OF是对角线两种情况进行讨论.利用三角函数即可求得N的坐标.
(1)在直角△OAC中,tan∠ACO=![]() ,
,
∴设OA=![]() x,则OC=3x,
x,则OC=3x,
根据勾股定理得:(3x)2+(![]() x)2=AC2,
x)2=AC2,
即9x2+3x2=576,
解得:x=4![]() .
.
则C的坐标是:(12![]() ,0),B的坐标是(
,0),B的坐标是(![]() );
);
(2)由折叠可知![]()
![]() ,
,
∵四边形![]() 是矩形,
是矩形,
∴![]() ∥
∥![]() ,
,
∴![]() ,
,
∴![]() =
=![]() ,
,
∴![]()
![]()
设直线![]() 的解析式为
的解析式为![]() ,则
,则![]() ,
,
解得![]() ;
;
∴![]() .
.
(3)∵OF为Rt△AOC斜边上的中线,
∴OF=![]() AC=12,
AC=12,
∵![]()
![]() ,
,
∴tan∠EDC=![]()
∴DE与x轴夹角是60°,
当FM是菱形的边时(如图1),ON∥FM,
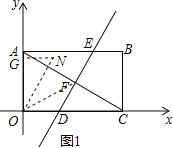
∴∠NOC=60°或120°.
当∠NOC=60°时,过N作NG⊥y轴,
∴NG=ONsin30°=12×![]() =6,OG=ONcos30°=12×
=6,OG=ONcos30°=12×![]() =6
=6![]() ,
,
此时N的坐标是(6,6![]() );
);
当∠NOC=120°时,与当∠NOC=60°时关于原点对称,则坐标是(-6,-6![]() );
);
当OF是对角线时(如图2),MN关于OF对称,
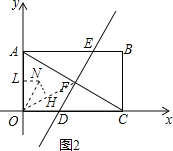
∵F的坐标是(6![]() ,6),
,6),
∴∠FOD=∠NOF=30°,
在直角△ONH中,OH=![]() OF=6,ON=
OF=6,ON=![]() .
.
作NL⊥y轴于点L.
在直角△ONL中,∠NOL=30°,
∴NL=![]() ON=
ON=![]() ,OL=ONcos30°=
,OL=ONcos30°=![]() ×
×![]() =6.
=6.
此时N的坐标是(/span>![]() ,6).
,6).
当DE与y轴的交点时M,这个时候N在第四象限,
此时点N的坐标为:(6![]() ,-6).
,-6).
则N的坐标是:(6![]() ,-6)或(6,6
,-6)或(6,6![]() )或(-6,-6
)或(-6,-6![]() )或(2
)或(2![]() ,6).
,6).
-
科目: 来源: 题型:
查看答案和解析>>【题目】下面各小题括号里的数,均是它前面的方程的解的是( )
A. 3x﹣1=5(2) B.
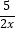 +1=0(﹣5,﹣7)
+1=0(﹣5,﹣7)C. x2﹣3x=4(4,1) D. x(x﹣2)(x+4)=0(2,4)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图(甲),在正方形
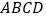 中,
中,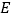 是
是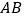 上一点,
上一点,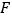 是
是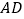 延长线上一点,且
延长线上一点,且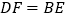 .
.(1)求证:
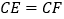 ;
;(2)在如图(甲)中,若
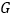 在
在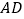 上,且
上,且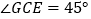 ,则
,则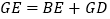 成立吗?
成立吗?证明你的结论.(3)运用(1)(2)解答中积累的经验和知识,完成下题:
如图(乙)四边形
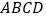 中,
中,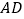 ∥
∥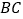 (
(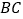 >
>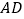 ),
),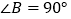 ,
,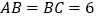 ,点
,点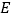 是
是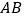 上一点,且
上一点,且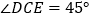 ,
,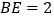 ,求
,求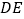 的长.
的长.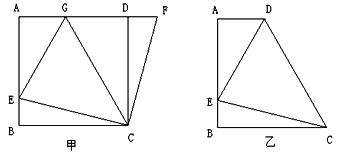
-
科目: 来源: 题型:
查看答案和解析>>【题目】某班将买一些乒乓球和乒乓球拍,现了解情况如下:甲、乙两家商店出售两种同样品牌的乒乓球和乒乓球拍.乒乓球拍每副定价30元,乒乓球每盒定价5元,经洽谈后,甲店每买一副球拍赠一盒乒乓球,乙店全部按定价的9折优惠.该班需球拍5副,乒乓球若干盒(不小于5盒).请解答下列问题:
(1)如果购买乒乓球
 (
( 不小于5)盒,则在甲店购买需付款 元,在乙店购买需付款 元。(用
不小于5)盒,则在甲店购买需付款 元,在乙店购买需付款 元。(用 的代数式表示)
的代数式表示)(2)当购买乒乓球多少盒时,在两店购买付款一样?
(3)如果给你450元,让你选择一家商店去办这件事,你打算去哪家商店购买?为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】甲、乙两家超市进行促销活动,甲超市采用“买100减50”的促销方式,即购买商品的总金额满100元但不足200元,少付50元;满200元但不足300元,少付100元;….乙超市采用“打6折”的促销方式,即顾客购买商品的总金额打6折.
(1)若顾客在甲商场购买商品的总金额为x(100≤x<200)元,优惠后得到商家的优惠率为p(p=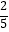 ),写出p与x之间的函数关系式,并说明p随x的变化情况;
),写出p与x之间的函数关系式,并说明p随x的变化情况;
(2)王强同学认为:如果顾客购买商品的总金额超过100元,实际上甲超市采用“打5折”、乙超市采用“打6折”,那么当然选择甲超市购物.请你举例反驳;
(3)品牌、质量、规格等都相同的某种商品,在甲乙两商场的标价都是x(300≤x<400)元,认为选择哪家商场购买商品花钱较少?请说明理由. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,已知关于x的二次函数y=x2+mx的图象经过原点O,并且与x轴交于点A,对称轴为直线x=1.
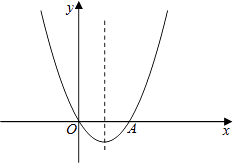
(1)常数m= , 点A的坐标为;
(2)若关于x的一元二次方程x2+mx=n(n为常数)有两个不相等的实数根,求n的取值范围;
(3)若关于x的一元二次方程x2+mx﹣k=0(k为常数)在﹣2<x<3的范围内有解,求k的取值范围. -
科目: 来源: 题型:
查看答案和解析>>【题目】下列函数的图象在每一个象限内,y值随x值的增大而增大的是( )
A.y=﹣x+1
B.y=x2﹣1
C.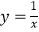
D.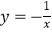
相关试题

