【题目】阅读、思考、解决问题：

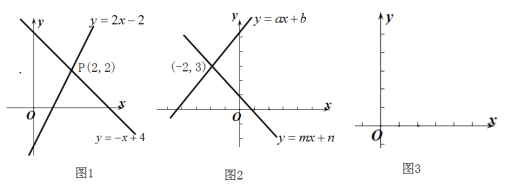
（1）如图（1）两个函数和的图象交于点，的坐标是否满足这两个函数式？即是方程的解吗？是方程的解吗？答： ① （是、不是）这就是说：函数和图象的交点坐标 ② （是、不是）方程组的解；反之，方程组的解 ③ （是、不是）函数和图象的交点坐标．

（2）根据图（2）写出方程组的解是：____________

（3）已知两个一次函数和．

①求这两个函数图象的交点坐标；

②在图（3）的坐标系中画出这两个函数的图象

③根据图象写出当时，的取值范围．

【答案】（1）是，是，是；（2）；（3）①（1，4）；②见解析；③x＞1.

【解析】

（1）根据两个一次函数图象的交点坐标与它们组成的二元一次方程组的解之间的关系进行解答即可；

（2）由函数图象中的交点坐标可得方程组的解；

（3）①求出这两个函数解析式组成的方程组的解即可；

②根据过点（0，3），过点（0，1），且这两个函数图象的交点坐标为：（1，4）画出函数图象即可；

③根据函数图象，找出的图象在的图象上方时x的取值范围即可.

解：（1）如图（1）两个函数和的图象交于点，的坐标是否满足这两个函数式？即是方程的解吗？是方程的解吗？答：是；这就是说：函数和图象的交点坐标是方程组的解；反之，方程组的解是函数和图象的交点坐标；

故答案为：是，是，是；

（2）由图（2）可得：方程组的解是：；

（3）①联立，解得：，

∴这两个函数图象的交点坐标为：（1，4）；

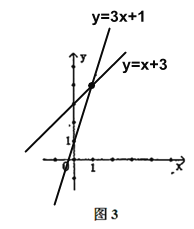
②易得过点（0，3），过点（0，1），且这两个函数图象的交点坐标为：（1，4），函数图象如图3所示：

③由函数图象可得：时，的取值范围是：x＞1.

关闭