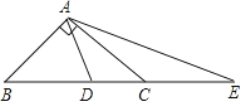
【题目】(1)如图,在△ABC中,∠BAC=90°,AB=AC,点D在BC上,且BD=BA,点E在BC的延长线上且CE=CA,试求∠DAE的度数;
(2))如果把第(1)题中“∠BAC=90°”的条件改为“∠BAC>90°”,其余条件不变,那么∠DAE与∠BAC有怎样的数量关系?
参考答案:
【答案】见解析
【解析】试题分析:
(1) 要求∠DAE的度数只要得到∠DAC与∠CAE的度数然后求和即可. 分析条件可知,△ABC,△ABD,△ACE均为等腰三角形. ∠B的度数易知,故∠BAD的度数可以在△ABD中由三角形内角和得到,进而可以得到∠DAC的度数. ∠ACB的度数易知,故∠CAE的度数可由三角形的外角关系得到. 这样即可求得∠DAE的度数.
(2) 通观第(1)小题的分析可知,∠DAE的度数实质上是由∠BAC的度数通过运算得到的. 分析本题的几何图形可知,第(2)小题所改变的条件并没有影响各角之间的几何关系. 因此,第(1)小题的思路可以用来求解∠DAE与∠BAC的数量关系. 求解时,参照第(1)小题的思路,将∠BAC当作代表角度的代数符号代入相应的式子进行运算,从而得到∠DAE与∠BAC的数量关系.
试题解析:
(1) ∠DAE=45°. 求解过程如下:
∵在△ABC中,∠BAC=90°,AB=AC,
∴∠B=∠ACB=45°,
∵AB=BD,
∴在△ABD中, ![]() ,
,
∴∠DAC=∠BAC-∠BAD=90°-67.5°=22.5°,
∵∠ACB是△ACE的一个外角,
∴∠ACB=∠CEA+∠CAE,
∵CE=CA,
∴![]() ,
,
∵∠ACB=45°,
∴![]() ,
,
∴∠DAE=∠DAC+∠CAE=22.5°+22.5°=45°.
(2) ![]() . 理由如下:
. 理由如下:
∵在△ABC中,AB=AC,
∴![]() ,
,
∵AB=BD,
∴在△ABD中, ![]() ,
,
∴![]() ,
,
∵∠DAC=∠BAC-∠BAD,
∴![]() ,
,
∵∠ACB是△ACE的一个外角,
∴∠ACB=∠CEA+∠CAE,
∵CE=CA,
∴在△ACE中, ![]() ,
,
∵![]() ,
,
∴![]() ,
,
∴![]() .
.
-
科目: 来源: 题型:
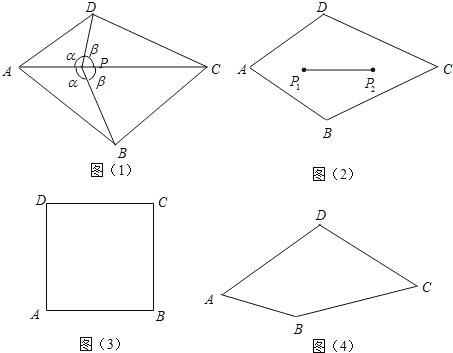
查看答案和解析>>【题目】如图(1),凸四边形ABCD,如果点P满足∠APD=∠APB=α.且∠BPC=∠CPD=β,则称点P为四边形ABCD的一个半等角点.
【1】在图(3)正方形ABCD内画一个半等角点P,且满足α≠β;
【2】在图(4)四边形ABCD中画出一个半等角点P,保留画图痕迹(不需写出画法);
【3】若四边形ABCD有两个半等角点P1、P2(如图(2)),证明线段P1P2上任一点也是它的半等角点.
-
科目: 来源: 题型:
查看答案和解析>>【题目】若x=2是方程8﹣2x=ax的解,则a=
-
科目: 来源: 题型:
查看答案和解析>>【题目】若关于x的一元一次方程2x+a﹣4=0的解是x=﹣2,则a的值是( )
A. ﹣8 B. 8 C. 2 D. 0
-
科目: 来源: 题型:
查看答案和解析>>【题目】南海是我国的南大门,如图所示,某天我国一艘海监执法船在南海海域正在进行常态化巡航,在A处测得北偏东30°方向上,距离为20海里的B处有一艘不明身份的船只正在向正东方向航行,便迅速沿北偏东75°的方向前往监视巡查,经过一段时间后,在C处成功拦截不明船只,问我海监执法船在前往监视巡查的过程中行驶了多少海里(最后结果保留整数)?
(参考数据:cos75°=0.2588,sin75°=0.9659,tan75°=3.732,
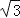 =1.732,
=1.732,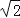 =1.414)
=1.414)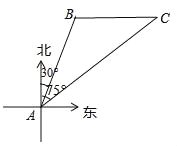
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知三角形的边长分别为4,a,8,则a的取值范围是________;如果这个三角形中有两条边相等,那么它的周长是______.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:15°37′+42°51′=
相关试题

