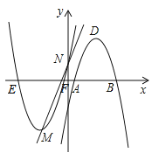
【题目】如图，在平面直角坐标系中，已知抛物线：的顶点为，与轴相交于点，先将抛物线沿轴翻折，再向右平移p个单位长度后得到抛物，直线；经过，两点．

（1）求点的坐标，并结合图象直接写出不等式：的解集；

（2）若抛物线的顶点与点关于原点对称，求p的值及抛物线的解析式；

（3）若抛物线与轴的交点为、（点、分别与抛物线上点、对应），试问四边形是何种特殊四边形？并说明其理由．

【答案】（1），；（2）4，；（3）平行四边形，见解析

【解析】

（1）利用配方法将抛物线C1的解析式配方，即可得出顶点M的坐标，结合函数图象的上下位置关系，即可得出不等式的解集；

（2）找出点M关于x轴对称的对称点的坐标，找出点M关于原点对称的对称点的坐标，二者横坐标做差即可得出p的值，根据抛物线的开口大小没变，开口方向改变，再结合平移后的抛物线的顶点坐标即可得出抛物线C2的解析式；

（3）由点的对称性知，DM、EB相互平分，故四边形EMBD是平行四边形．

解：（1）

观察函数图象，发现：当﹣2＜x＜0时，抛物线C1在直线l的下方，

∴不等式的解集是；

（2）关于对称的点为

点与点关于原点对称

抛物线与的形状相同，开口相反

值互为相反数

抛物线的顶点

；

（3）令y＝x2+6x+2＝0，则x＝﹣2，

即点E、F的坐标分别为（﹣2﹣，0）、（﹣2+，0），

点M（﹣2，﹣4）；

同理点A、B、D的坐标分别为（2﹣，0）、（2+，0）、（2，4），

由点的对称性知，DM、EB相互平分，故四边形EMBD是平行四边形，

关闭