【题目】已知关于x、y的二元一次方程组x-y=3a①和x+3y=4-a②.
(1)如果![]() 是方程①的解,求a的值;
是方程①的解,求a的值;
(2)当a=1时,求两个方程的公共解;
(3)若方程组![]() 的解满足x≤0,求y的取值范围.
的解满足x≤0,求y的取值范围.
参考答案:
【答案】(1)-1;(2)x=3,y=0;(3)y≥![]()
【解析】
(1)将题目中的二元一次方程组的解代入方程①,解关于a的方程即可.
(2)将a=1代入方程,利用加减法解方程组即可;
(3)将x,y用a表示出来,即可得到答案.
(1)由题意得2-5=3a,
解得a=-1.
(2)当a=1时,则有
②-①得:4y=0,
解得y=0,
把y=0代入①得x=3,
所以,两方程的公共解是![]() ;
;
(3)解方程组![]() 得
得![]() ,
,
∵x≤0,
∴2a+1≤0,
∴a≤-![]() ,
,
所以1-a≥![]() ,
,
∴y≥![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,矩形OABC的两边在坐标轴上,连接AC,抛物线y=x2-4x-2经过A,B两点.
(1)求A点坐标及线段AB的长;
(2)若点P由点A出发以每秒1个单位的速度沿AB边向点B移动,1秒后点Q也由点A出发以每秒7个单位的速度沿A-O-C-B的方向向点B移动,当其中一个点到达终点时另一个点也停止移动,点P的移动时间为t秒.
①当PQ⊥AC时,求t的值;
②当PQ∥AC时,对于抛物线对称轴上一点H,当点H的纵坐标满足条件_________时,∠HOQ<∠POQ.(直接写出答案)

-
科目: 来源: 题型:
查看答案和解析>>【题目】已知,如图,在△ABC和△DEF(它们均为锐角三角形)中,AC=DF,AB=DE.
(1)用尺规在图中分别作出AB、DE边上的高CG、FH(不要写作法,保留作图痕迹).
(2)如果CG=FH,猜测△ABC和△DEF是否全等,并说明理由。

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,正方形ABCD的一边AB在直尺一边所在直线MN上,点O是对角线AC、BD的交点,过点O作OE⊥MN于点E.

(1)如图1,线段AB与OE之间的数量关系为 .(请直接填结论)
(2)保证点A始终在直线MN上,正方形ABCD绕点A旋转θ(0<θ<90°),过点 B作BF⊥MN于点F.
①如图2,当点O、B两点均在直线MN右侧时,试猜想线段AF、BF与OE之间存在怎样的数量关系?请说明理由.
②如图3,当点O、B两点分别在直线MN两侧时,此时①中结论是否依然成立呢?若成立,请直接写出结论;若不成立,请写出变化后的结论并证明.
③当正方形ABCD绕点A旋转到如图4的位置时,线段AF、BF与OE之间的数量关系为 .(请直接填结论)
-
科目: 来源: 题型:
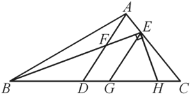
查看答案和解析>>【题目】如图,在△ABC中,已知∠ABC=30°,点D在BC上,点E在AC上,∠BAD=∠EBC, AD交BE于F.
(1)求∠BFD的度数;
(2)若EG∥AD交BC于G,EH⊥BE交BC于H,求∠HEG的度数.
-
科目: 来源: 题型:
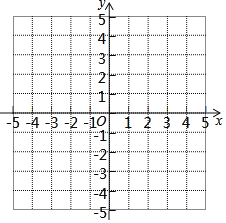
查看答案和解析>>【题目】已知在平面直角坐标系中有三点A(﹣2,1),B(3,1),C(2,3),请解答下列问题:
(1)在坐标系内描出A,B,C的位置;
(2)画出△ABC关于x轴对称的图形△A1B1C1,并写出顶点A1,B1,C1的坐标;
(3)写出∠C的度数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在△ABC中,AD⊥BC,垂足为D,AD=CD,点E在AD上,DE=BD,M、N分别是AB、CE的中点.
(1)求证:△ADB≌△CDE;
(2)求∠MDN的度数.

相关试题

