【题目】某商场试销一种成本为每件120元的服装,规定试销期间销售单价不低于成本单价,且获利不得高于45%,经试销发现,销售量![]() (件)是销售单价
(件)是销售单价![]() (元)的函数,并且满足如下对应值表:
(元)的函数,并且满足如下对应值表:
销售单价 | 130 | 140 | 145 |
销售量 | 110 | 100 | 95 |
(1)求![]() 与
与![]() 的函数表达式;
的函数表达式;
(2)若该商场获得利润为![]() 元,试写出利润
元,试写出利润![]() 与销售单价
与销售单价![]() 之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
之间的关系式;销售单价定为多少元时,商场可获得最大利润,最大利润是多少元?
(3)若该商场获得利润不低于 2000元,试确定销售单价![]() 的范围.
的范围.
参考答案:
【答案】(1)![]() ;(2)
;(2)![]() ,定价为174元时,利润最大为3564元;(3)
,定价为174元时,利润最大为3564元;(3)![]() .
.
【解析】试题分析: (1)列出二元一次方程组解出k与b的值可求出一次函数的表达式.
(2)依题意求出W与x的函数表达式可推出当x=174时商场可获得最大利润.
(3)由w=2000推出x300x+16400=0x2-180x+7700=0解出x的值即可.
试题解析:
(1)根据题意得![]()
解得k=1,b=240.
所求一次函数的表达式为y=x+240.
(2)W=(x120)(x+240)=x+360x28800=(x180) +3600,
∵抛物线的开口向下,
∴当x<150时,W随x的增大而增大,
而销售单价不低于成本单价,且获利不得高于45%,
即120x120×(1+45%),
∴120x174,
∴当x=174时,W=(174180) +3600=3564.
∴当销售单价定为174元时,商场可获得最大利润,最大利润是3564元.
(3)由W2000,得2000(x180) +3600,
整理得,x360x+308000,
而方程x360x+30800=0的解为x =140,x =220.
即x =140,x =220时利润为2000元,而函数y= x360x+30800的开口向下,所以要使该商场获得利润不低于2000元,销售单价应在140元到220元之间,
而120元/件x174元/件,所以,销售单价x的范围是140元/件x174元/件。
-
科目: 来源: 题型:
查看答案和解析>>【题目】央视2月8日报道,除夕夜春晚直播期间的观众总规模达10.33亿,10.33亿用科学记数法表示为 .
-
科目: 来源: 题型:
查看答案和解析>>【题目】某超市将甲、乙两种商品进价各自提价30%后,又同时降价30元出售,售出后两种商品的总利润为60元,则甲、乙两种商品进价之和为元.
-
科目: 来源: 题型:
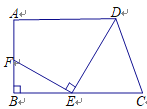
查看答案和解析>>【题目】如图,在梯形ABCD中,已知AD∥BC,∠B=90°,AB=7,AD=9,BC=12,在线段BC上任取一点E,连接DE,作EF⊥DE,交直线AB于点F.
(1)若点F与B重合,求CE的长;(3分)
(2)若点F在线段AB上,且AF=CE,求CE的长.(5分)
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,我市云台山景区内一条笔直的公路a经过三个景点A、B、C,现在市政府决定开发风景优美的景点D.经测量景点D位于景点A的北偏东30方向12km处,位于景点B的正北方向,还位于景点C的北偏西75方向上.已知AB=
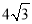 km.
km.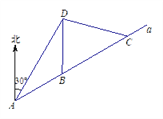
(1)现准备由景点D向公路a修建一条距离最短的公路,不考虑其他因素,求出这条公路的长;
(2)求出景点B与景点C之间的距离(结果保留根号).
-
科目: 来源: 题型:
查看答案和解析>>【题目】在国家倡导下,“全民阅读”正逐步走向普及,学校要求同学们在家里利用闲暇时光多读些有益的书籍. 王刚同学在本学期开学初对本年级部分同学寒假在家平均每天读书的页数进行了抽样调查(结果取整数),所得数据统计如下表:
读书页数
0.5~20.5
20.5~40.5
40.5~60.5
60.5~80.5
80.5~100.5
频 数
20
25
30
15
10
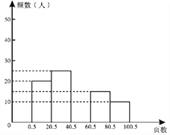
(1)抽取样本的容量是 .
(2)根据表中数据补全图中的频数分布直方图.
(3)样本的中位数所在的范围是 .
(4)若该年级有学生1060人,那么大约有多少学生在寒假平均每天读书60.5~100.5页之间?
-
科目: 来源: 题型:
查看答案和解析>>【题目】把多项式5x2y3﹣2x4y2+7+3x5y按x的降幂排列后,第三项是( )
A.5x2y3
B.﹣2x4y2
C.7
D.3x5y
相关试题

