【题目】已知:在四边形![]() 中,
中, ![]() ,
, ![]() ,
, ![]() ,
, ![]() .
.
(![]() )求四边形
)求四边形![]() 的面积.
的面积.
(![]() )点
)点![]() 是线段
是线段![]() 上的动点,连接
上的动点,连接![]() 、
、![]() ,求
,求![]() 周长的最小值及此时
周长的最小值及此时![]() 的长.
的长.

(![]() )点
)点![]() 是线段
是线段![]() 上的动点,
上的动点, ![]() 、
、![]() 为边
为边![]() 上的点,
上的点, ![]() ,连接
,连接![]() 、
、![]() ,分别交
,分别交![]() 、
、![]() 于点
于点![]() 、
、![]() ,记
,记![]() 和
和![]() 重叠部分的面积为
重叠部分的面积为![]() ,求
,求![]() 的最值.
的最值.

参考答案:
【答案】(![]() )
)![]() .(
.(![]() )
)![]() .3.(
.3.(![]() )
)![]() .
.
【解析】试题分析:(1)如图1,过A作AE⊥BC于E,DF⊥BC于F,得到四边形AEFD是矩形,由矩形的想知道的EF=AD=6,BE=CF=3,根据勾股定理得到![]() ,于是得到结论;
,于是得到结论;
(2)如图2,作点B关于直线AD的对称点G,连接CG交AD于P,则BC+PB+PC=BC+PG+PC即为△BCP周长的最小值,根据勾股定理得到![]() ,于是得到△BCP周长的最小值为:4
,于是得到△BCP周长的最小值为:4![]() +12;根据三角形中位线的性质得到PH=
+12;根据三角形中位线的性质得到PH=![]() BC=6,由勾股定理得到
BC=6,由勾股定理得到![]() ,于是得到结论.
,于是得到结论.
(3)过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,过
点,过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,过
点,过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,如图所示,设
点,如图所示,设![]() ,则
,则![]() .因为
.因为![]() ,所以
,所以![]() ∽
∽![]() ,得
,得![]() ;同理可得
;同理可得![]() ∽
∽![]() ,
, ![]() ∽
∽![]() ,得:
,得: ![]() ,
, ![]() ,所以
,所以![]() ,进而求得答案.
,进而求得答案.
试题解析:(![]() )如图1,过
)如图1,过![]() 作
作![]() 于
于![]() ,
, ![]() 于
于![]() .
.

则四边形![]() 是矩形.
是矩形.
∴![]() ,
, ![]() .
.
∴![]() .
.
∴![]() .
.
(![]() )如图2,作点
)如图2,作点![]() 关于直线
关于直线![]() 的对称点
的对称点![]() ,
,

连接![]() 交
交![]() 于
于![]() ,则
,则![]() .
.
即为![]() 的最小周长.
的最小周长.
由(![]() )知
)知![]() .
.
在![]() 中,
中, ![]() .
.
∴![]() 的
的![]() .
.
∵![]() ,
, ![]() ,
,
∴![]() .
.
∵![]() ,
,
∴![]() .
.
(![]() )过
)过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,过
点,过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,过
点,过![]() 点作
点作![]() 的垂线分别交
的垂线分别交![]() 、
、![]() 于
于![]() 、
、![]() 点,如图3所示,设
点,如图3所示,设![]() ,则
,则![]() .
.

因为![]() ,所以
,所以![]() ∽
∽![]() ,
,
所以![]() ,又
,又![]() ,所以
,所以![]() ;
;
同理可得![]() ∽
∽![]() ,
, ![]() ∽
∽![]() ,
,
所以![]() ,
, ![]() ,
,
求得: ![]() ,
, ![]() ,其中
,其中![]() ,
,
所以![]() ,
,
即![]()
![]() .
.
因此当![]() 时,
时, ![]() 有最大值
有最大值![]() ;当
;当![]() 或
或![]() 时,
时, ![]() 有最小值了
有最小值了![]() .
.
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知∠A=35°10′48″,则∠A的补角是°.
-
科目: 来源: 题型:
查看答案和解析>>【题目】保障房建设是民心工程,某市从2008年开始加快保障房建设进程,现统计了该市2008年到2012年这5年新建保障房情况,绘制成如图所示的折线统计图和不完整的条形统计图.
(1)小丽看了统计图后说:“该市2011年新建保障房的套数比2010年少了.”你认为小丽说法正确吗?请说明理由;
(2)求补全条形统计图;
(3)求这5年平均每年新建保障房的套数.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图
 ,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字
,一枚质地均匀的正四面体骰子,它有四个面并分别标有数字 ,
, ,
, ,
, ,如图
,如图 ,正方形
,正方形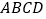 顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图
顶点处各有一个圈.跳圈游戏的规则为:游戏者每掷一次骰子,骰子着地一面上的数字是几,就沿正方形的边顺时针方向连续跳几个边长.如:若从图 起跳,第一次掷得
起跳,第一次掷得 ,就顺时针连续跳
,就顺时针连续跳 个边长,落到圈
个边长,落到圈 ;若第二次掷得
;若第二次掷得 ,就从
,就从 开始顺时针连续跳
开始顺时针连续跳 个边长,落到圈
个边长,落到圈 ;
; 设游戏者从圈
设游戏者从圈 起跳.
起跳.(
 )嘉嘉随机掷一次骰子,求落回到圈
)嘉嘉随机掷一次骰子,求落回到圈 的概率
的概率 .
.(
 )淇淇随机掷两次骰子,用列表法求最后落回到圈
)淇淇随机掷两次骰子,用列表法求最后落回到圈 的概率
的概率 ,并指出她与嘉嘉落回到圈
,并指出她与嘉嘉落回到圈 的可能性一样吗?
的可能性一样吗?
-
科目: 来源: 题型:
查看答案和解析>>【题目】两船从同一港口同时出发反向而行,甲船顺水,乙船逆水,两船在静水中的速度都是50千米/时,水流速度是a千米/时,2小时后甲船比乙船多航行_____千米.
-
科目: 来源: 题型:
查看答案和解析>>【题目】平面直角坐标系
 中,对称轴平行与
中,对称轴平行与 轴的抛物线过点
轴的抛物线过点 、
、 和
和 .
.(
 )求抛物线的表达式.
)求抛物线的表达式.(
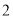 )现将此抛物线先沿
)现将此抛物线先沿 轴方向向右平移
轴方向向右平移 个单位,再沿
个单位,再沿 轴方向平移
轴方向平移 个单位,若所得抛物线与
个单位,若所得抛物线与 轴交于点
轴交于点 、
、 (点
(点 在点
在点 的左边),且使
的左边),且使 (顶点
(顶点 、
、 、
、 依次对应顶点
依次对应顶点 、
、 、
、 ),试求
),试求 的值,并说明方向.
的值,并说明方向.
-
科目: 来源: 题型:
查看答案和解析>>【题目】计算:(1)5﹣(﹣8);(2)﹣22+3×(﹣1)2018﹣9÷(﹣3).
相关试题

