Question

【题目】在平面直角坐标系xOy中，抛物线y=﹣x2+2mx﹣m2+1的对称轴是直线x=1．

（1）求抛物线的表达式；

（2）点D（n，y1），E（3，y2）在抛物线上，若y1＜y2，请直接写出n的取值范围；

（3）设点M（p，q）为抛物线上的一个动点，当﹣1＜p＜2时，点M关于y轴的对称点都在直线y=kx﹣4的上方，求k的取值范围．

Answer 1

【答案】（1）抛物线的解析式为y=﹣x2+2x．（2）当n＜﹣1或n＞3时，y1＜y2．

（3）∴k的取值范围是﹣2≤k≤1．

【解析】

试题分析：（1）由抛物线的对称轴方程可求得m=1，从而可求得抛物线的表达式；

（2）将x=3代入抛物线的解析式，可求得y2=3，将y=3代入抛物线的解析式可求得x1=﹣1，x2=3，由抛物线的开口向下，可知当当n＜﹣1或n＞3时，y1＜y2；

（3）先根据题意画出点M关于y轴对称点M′的轨迹，然后根据点M关于y轴的对称点都在直线y=kx﹣4的上方，列出关于k的不等式组即可求得k的取值范围．

试题解析：（1）∵抛物线的对称轴为x=1，∴x=﹣=1．

解得：m=1．∴抛物线的解析式为y=﹣x2+2x．

（2）将x=3代入抛物线的解析式得y=﹣32+2×3=﹣3．

将y=﹣3代入得：﹣x2+2x=﹣3．解得：x1=﹣1，x2=3．

∵a=﹣1＜0，∴当n＜﹣1或n＞3时，y1＜y2．

（3）设点M关于y轴对称点为M′，则点M′运动的轨迹如图所示：

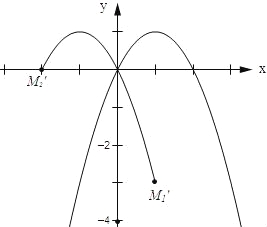
∵当P=﹣1时，q=﹣（﹣1）2+2×（﹣1）=﹣3．∴点M关于y轴的对称点M1′的坐标为（1，﹣3）．

∵当P=2时，q=﹣22+2×2=0，∴点M关于y轴的对称点M2′的坐标为（﹣2，0）．

①当k＜0时，∵点M关于y轴的对称点都在直线y=kx﹣4的上方，∴﹣2k﹣4≤0．

解得：k≥﹣2．

②当k＞0时，∵点M关于y轴的对称点都在直线y=kx﹣4的上方，

∴k﹣4≤﹣3．解得；k≤1．

∴k的取值范围是﹣2≤k≤1．