搜索
【题目】下列方程中，有两个不相等实数根的是（ ）
A. x2－2x－1=0 B. x2－2x+3=0 C. x2=2
x－3 D. x2－4x+4=0
参考答案：
【答案】A
【解析】试题分析：分别计算出各项中方程根的判别式的值，找出大于0的选项即可：
A、a=1，b=﹣2，c=﹣1，
∵△=b2﹣4ac=5＞0，∴方程有两个不相等的实数根，本选项符合题意；
B、a=1，b=﹣2，c=3，
∵△=b2﹣4ac=﹣8＜0，∴方程没有实数根，本选项不合题意；
C、移项，得x2－2
x+3=0，a=1，b=﹣2
，c=3，
∵△=b2﹣4ac=0，∴方程有两个相等的实数根，本选项不合题意；
D、a=1，b=﹣4，c=4，
∵△=b2﹣4ac=0，∴方程有两个相等的实数根，本选项不合题意.
故选A.
-
科目： 来源： 题型：
查看答案和解析>>【题目】解方程：（1）6x
-7x+1=0；（2）4x-3x=52；（3）（x-2）（x-3）=12；（4）5x
-18=9x -
科目： 来源： 题型：
查看答案和解析>>【题目】在□ABCD中，AC、BD交于点O，过点O作直线EF、GH，分别交平行四边形的四条边于E、G、F、H四点，连接EG、GF、FH、HE．
（1）如图①，试判断四边形EGFH的形状，并说明理由；
（2）如图②，当EF⊥GH时，四边形EGFH的形状是 ；
（3）如图③，在（2）的条件下，若AC=BD，四边形EGFH的形状是 ；
（4）如图④，在（3）的条件下，若AC⊥BD，试判断四边形EGFH的形状，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图1在正方形ABCD中，P是对角线BD上的一点，点E在AD的延长线上，且PA=PE，PE交CD于F.
（1）证明：PC=PE；
（2）求∠CPE的度数；
（3）如图2，把正方形ABCD改为菱形ABCD，其他条件不变，当∠ABC=120度时，连接CE，试探究线段AP与线段CE的数量关系，并说明理由.
-
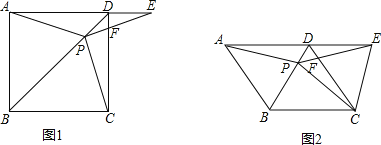
科目： 来源： 题型：
查看答案和解析>>【题目】如图，在正方形ABCD中，点E，F分别在边AB，BC上，∠ADE＝∠CDF.
(1)求证：AE＝CF；
(2)连接DB交EF于点O，延长OB至G，使OG＝OD，连接EG，FG，判断四边形DEGF是否是菱形，并说明理由．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，已知，BD为△ABC的角平分线，且BD=BC，E为BD延长线上的一点，BE=BA．下列结论：①△ABD≌△EBC；②AC=2CD；③AD=AE=EC；④∠BCE+∠BCD=180°．其中正确的是
A. ①②③ B. ①②④ C. ①③④ D. ②③④
-
科目： 来源： 题型：
查看答案和解析>>【题目】已知两圆相交，它们的圆心距为3，一个圆的半径是2，那么另一个圆的半径长可以是（ ）
A.1
B.3
C.5
D.7
相关试题
