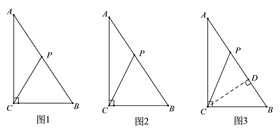
【题目】如图,△ABC中,∠ACB=90°,AC=4,BC=3,点P是AB边上一动点.
当△PCB是等腰三角形时,求AP的长度.

参考答案:
【答案】AP的长为2.5或2或1.4.
【解析】试题分析:
当△PCB为等腰三角形时,存在3种情况:①PC=PB、②BC=BP、③CB=CP,结合已知条件分上面三种情况讨论解出对应的AP长度即可.
试题解析:
∵在△ABC中,∠ACB=90°,AC=4,BC=3,
∴AB=![]() =5.
=5.
当△PCB为等腰三角形时,存在3种情况:①PC=PB、②BC=BP、③CB=CP,现分别讨论如下:
① 如图1,在△ABC中,∵∠ACB=90°,
∴当点P是AB的中点时,PC=PB=AP=![]() AB,△PCB是等腰三角形,此时:AP=
AB,△PCB是等腰三角形,此时:AP=![]() AB =2.5;
AB =2.5;
② 如图2,当BP=BC=3时,△PCB是等腰三角形,此时AP=AB-BC=5-3=2;
③ 如图3,当CB=CP时,△PCB是等腰三角形,此时过点C作CD⊥AB于点D,则DP=DB,
∵在△ABC中, ![]() ,
,
∴![]() ,解得CD=2.4.
,解得CD=2.4.
∴在Rt△CBD中,利用勾股定理可得:BD=![]() =1.8.
=1.8.
∴ BP=2BD=3.6.
∴ AP=AB-BP=1.4.
综上上述:若△PCB是等腰三角形,则AP的长为2.5或2或1.4.
-
科目: 来源: 题型:
查看答案和解析>>【题目】全球新冠肺炎确诊人数截止到4月30日止约有220万人,用科学记数法表示220万人为( )
A.220×104人B.2.20×107人
C.2.20×106人D.0.220×107人
-
科目: 来源: 题型:
查看答案和解析>>【题目】一方有难八方支援,某市政府筹集了抗旱必需物资120吨打算运往灾区,现有甲、乙、丙三种车型供选择,每辆车的运载能力和运费如下表所示:(假设每辆车均满载)
车型
甲
乙
丙
汽车运载量(吨/辆)
5
8
10
汽车运费(元/辆)
400
500
600
(1)若全部物资都用甲、乙两种车型来运送,需运费8200元,问分别需甲、乙两种车型各几辆?
(2)为了节约运费,该市政府可以调用甲、乙、丙三种车型参与运送,已知它们的总辆数为16辆,你能通过列方程组的方法分别求出几种车型的辆数吗?
(3)求出那种方案的运费最省?最省是多少元. -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,某测量人员的眼睛A与标杆顶端F、电视塔顶端E在同一条直线上,已知此人的眼睛到地面的距离AB=1.6m,标杆FC=2.2m,且BC=1m,CD=5m,标杆FC、ED垂直于地面.求电视塔的高ED.

-
科目: 来源: 题型:
查看答案和解析>>【题目】下列运算正确的是( )
A.(﹣a3)2=a6B.2a+3b=5ab
C.(a+1)2=a2+1D.a2a3=a6
-
科目: 来源: 题型:
查看答案和解析>>【题目】下列说法正确的是( )
A. 整数就是正整数和负整数 B. 分数包括正分数和负分数
C. 在有理数中,不是负数就是正数 D. 零是整数,但不是自然数
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知方程组
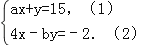 甲由于看错了方程(1)中的a,得到方程组的解为
甲由于看错了方程(1)中的a,得到方程组的解为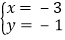 , 乙由于看错了方程(2)中的b,得到方程组的解为
, 乙由于看错了方程(2)中的b,得到方程组的解为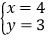 , 若按正确的计算,求x+6y的值.
, 若按正确的计算,求x+6y的值.
相关试题

