Question

【题目】求证：等腰三角形底边上任一点到两腰的距离之和等于腰上的高.

Answer 1

【答案】（1）证明见解析.

【解析】试题分析：根据三角形的面积公式S△=底×高求得S△ABD、S△ACD、S△ABC；又由图易知，S△ABC=S△ABD+S△ACD，分析到这里，问题就迎刃而解了．

试题解析：已知：△ABC中，AB=AC，D为BC上任意一点，DE⊥AB，DF⊥AC，垂足为E.F，CG⊥AB于G，

求证：CG=DE+DF.

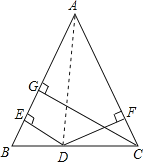
证明：已知如图所示。

∵ED⊥AB，

∴S△ABD=ABED；

∵DF⊥AC，

∴S△ACD=ACDF；

∵CG⊥AB，

∴S△ABC=ABCG；

又∵AB=AC,S△ABC=S△ABD+S△ACD，

∴ABCG=ABED+ACDF，

∴CG=DE+DF.