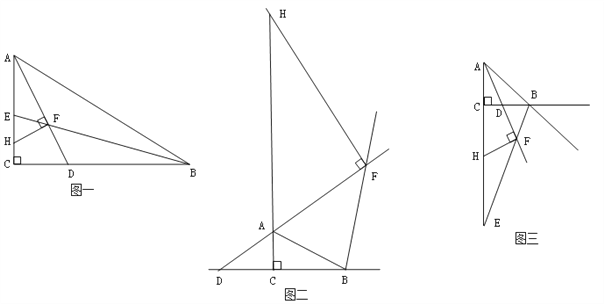
【题目】如图一:在Rt△ABC中,∠C=90°AD、BE分别是△ABC中∠A、∠B的平分线,AD、BE交于点F,过F点做FH⊥AD交AC于点H,易证:AH+DB=AB;
(1)若将Rt△ABC中∠BAC、∠ABC的内角平分线改成外角平分线,即:AF、BF分别是∠BAC、∠ABC的外角平分线交于F点,FH⊥AF交直线AC于H点,如图二:请写出线段AH、BD、AB之间的数量关系,并证明。
(2)若将Rt△ABC中∠BAC、∠ABC的内角平分线改成一个是外角平分线,即:AF是∠A的内角平分线,BE是∠B的外角平分线交于F点,FH⊥AD交AC于点H.如图三:请写出线段AH、BD、AB之间的数量关系,无需证明。
参考答案:
【答案】(1) AH=AB+BD ,证明见解析;(2) AH=AB+BD
【解析】(1)的结论是:AH=AB+BD
(2)的结论是:AH=AB+BD
(1)的结论证明如下:
∵AF平分∠BAH
∴∠BAF=∠HAF
∵AF⊥HM
∴△HAF≌△MAF
∴AH=AM ∠AHF=∠M
∵AF平分∠BAH
∴∠ABF=∠FBN
∵∠AHF+∠HAF=90°
∵∠DAC+∠ADB=90°
∴∠ADB=∠AHF
∴∠FDB=∠BMF
∴△DFB≌△MFB
∴DB=BM
∵AM=AB+BM
∴AH=AB+DB
-
科目: 来源: 题型:
查看答案和解析>>【题目】用度、分、秒表示51.23°为__________________
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,P为Rt△ABC所在平面内任意一点(不在直线AC上),∠ACB=90°,M为AB边中点.操作:以PA、PC为邻边作平行四边形PADC,连续PM并延长到点E,使ME=PM,连接DE. 探究:
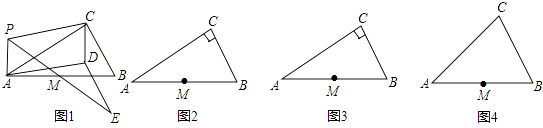
(1)请猜想与线段DE有关的三个结论;
(2)请你利用图2,图3选择不同位置的点P按上述方法操作;
(3)经历(2)之后,如果你认为你写的结论是正确的,请加以证明; 如果你认为你写的结论是错误的,请用图2或图3加以说明;
(注意:错误的结论,只要你用反例给予说明也得分)
(4)若将“Rt△ABC”改为“任意△ABC”,其他条件不变,利用图4操作,并写出与线段DE有关的结论(直接写答案). -
科目: 来源: 题型:
查看答案和解析>>【题目】点A(a,4),点B(3,b)关于x轴对称,则(a+b)2013的值为 ( )
A. 0 B. -1 C. 1 D. 72013
-
科目: 来源: 题型:
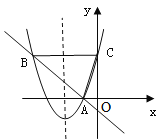
查看答案和解析>>【题目】已知:抛物线y=x2+4x+4+m的图像与y轴交于点C,点B与点C的纵坐标相同,一次函数y=kx+b的与二次函数交于A、B两点,且A点坐标为(-1,0).
(1)求二次函数与一次函数的解析式;
(2)若抛物线对称轴上存在一点P,直线PC将△ABC分成面积为1:2两部分,求P点坐标。
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F是对角线BD上的两点,如果添加一个条件使△ABE≌△CDF,则添加的条件
 是( )
是( ) 
A.AE=CF
B.BE=FD
C.BF=DE
D.∠1=∠2 -
科目: 来源: 题型:
查看答案和解析>>【题目】为建设秀美龙江,某学校组织师生参加一年一度的植树绿化工作,准备租用7辆客车,现有甲、乙两种客车,它们的载客量和租金如下表,设租用甲种客车x辆,租车总费用为y元,
甲种客车
乙种客车
载客量/(人/辆)
60
40
租金/(元/辆)
360
300
(1)求出y(单位:元)与x(单位:辆)之间的函数关系式。
(2)若该校共有350名师生前往参加劳动,共有多少种租车方案?
(3)带队老师从学校预支租车费用2400元,试问预支的租车费用是否可有结余?若有结余,最多可结余多少元。
相关试题

