【题目】已知,ABCD中,∠ABC=90°,AB=4cm,BC=8cm,AC的垂直平分线EF分别交AD、BC于点E、F,垂足为O.

(1)如图1,连接AF、CE.求证:四边形AFCE为菱形.
(2)如图1,求AF的长.
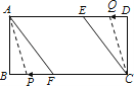
(3)如图2,动点P、Q分别从A、C两点同时出发,沿△AFB和△CDE各边匀速运动一周.即点P自A→F→B→A停止,点Q自C→D→E→C停止,在运动过程中,点P的速度为每秒1cm,点Q的速度为每秒0.8cm,设运动时间为t秒,若当以A、P、C、Q四点为顶点的四边形是平行四边形时,求t的值.
参考答案:
【答案】(1)证明见解析;(2)AF=5;(3)以A,C,P,Q四点为顶点的四边形是平行四边形时,t=![]() 秒.
秒.
【解析】
(1)先证明四边形![]() 为平行四边形,再根据对角线互相垂直平分的四边形是菱形作出判定;
为平行四边形,再根据对角线互相垂直平分的四边形是菱形作出判定;
(2)根据勾股定理即可求![]() 的长;
的长;
(3)分情况讨论可知,![]() 点在
点在![]() 上,
上,![]() 点在
点在![]() 上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可;
上时,才能构成平行四边形,根据平行四边形的性质列出方程求解即可;
解:(1)![]() 四边形
四边形![]() 是矩形,
是矩形,
![]() ,
,
![]() ,
,![]() .
.
![]() 垂直平分
垂直平分![]() ,
,
![]() .
.
在![]() 和
和![]() 中,
中,
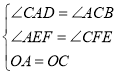 ,
,
![]() ,
,
![]() .
.
![]() ,
,
![]() 四边形
四边形![]() 是平行四边形,
是平行四边形,
![]() ,
,
![]() 四边形
四边形![]() 为菱形.
为菱形.
(2)设菱形的边长![]() ,则
,则![]() ,
,
在![]() 中,
中,![]() ,由勾股定理,得
,由勾股定理,得
![]() ,
,
解得:![]() ,
,
![]() .
.
(3)由作图可以知道,![]() 点
点![]() 上时,
上时,![]() 点
点![]() 上,此时
上,此时![]() ,
,![]() ,
,![]() ,
,![]() 四点不可能构成平行四边形;
四点不可能构成平行四边形;
同理![]() 点
点![]() 上时,
上时,![]() 点
点![]() 或
或![]() 上,也不能构成平行四边形.
上,也不能构成平行四边形.
![]() 只有当
只有当![]() 点在
点在![]() 上,
上,![]() 点在
点在![]() 上时,才能构成平行四边形,
上时,才能构成平行四边形,
![]() 以
以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,
![]() ,
,
![]() 点
点![]() 的速度为每秒
的速度为每秒![]() ,点
,点![]() 的速度为每秒
的速度为每秒![]() ,运动时间为
,运动时间为![]() 秒,
秒,
![]() ,
,![]() ,
,
![]() ,
,
解得:![]() .
.
![]() 以
以![]() ,
,![]() ,
,![]() ,
,![]() 四点为顶点的四边形是平行四边形时,
四点为顶点的四边形是平行四边形时,![]() 秒.
秒.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某风景区计划在绿化区域种植银杏树,现甲、乙两家有相同的银杏树苗可供选择,其具体销售方案如下:
甲
乙
购树苗数量
销售单价
购树苗数量
销售单价
不超过500棵时
800元/棵
不超过1000棵时
800元/棵
超过500棵的部分
700元/棵
超过1000棵的部分
600元/棵
设购买银杏树苗x棵,到两家购买所需费用分别为y甲元、y乙元
(1)该风景区需要购买800棵银杏树苗,若都在甲家购买所要费用为 元,若都在乙家购买所需费用为 元;
(2)当x>1000时,分别求出y甲、y乙与x之间的函数关系式;
(3)如果你是该风景区的负责人,购买树苗时有什么方案,为什么?
-
科目: 来源: 题型:
查看答案和解析>>【题目】【问题原型】如图1,在四边形ABCD中,∠ADC=90°,AB=AC.点E、F分别为AC、BC的中点,连结EF,DE.试说明:DE=EF.
【探究】如图2,在问题原型的条件下,当AC平分∠BAD,∠DEF=90°时,求∠BAD的大小.
【应用】如图3,在问题原型的条件下,当AB=2,且四边形CDEF是菱形时,直接写出四边形ABCD的面积.

-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,平行四边形ABCD中,E,F分别为AD,BC边上的一点,增加下列条件,不能得出BE∥DF的是( )

A. AE=CF B. BE=DF C. ∠EBF=∠FDE D. ∠BED=∠BFD
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,在平面直角坐标系中,OA=AB,∠OAB=90°,反比例函数y=
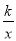 (x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为_____.
(x>0)的图象经过A,B两点.若点A的坐标为(n,1),则k的值为_____.
-
科目: 来源: 题型:
查看答案和解析>>【题目】 “囧”(jiong)是近时期网络流行语,像一个人脸郁闷的神情.如图所示,一张边长为20的正方形的纸片,剪去两个一样的小直角三角形和一个长方形得到一个“囧”字图案(阴影部分).设剪去的小长方形长和宽分别为x、y,剪去的两个小直角三角形的两直角边长也分别为x、y.
(1)用含有x、y的代数式表示右图中“囧”的面积;
(2)当
 时,求此时“囧”的面积.
时,求此时“囧”的面积.
-
科目: 来源: 题型:
查看答案和解析>>【题目】某校为更好的开展“春季趣味运动会”活动,随机在各年级抽查了部分学生,了解他们最喜爱的趣味运动项目类型(跳绳、实心球、50m、拔河共四类),并将统计结果绘制成如下不完整的频数分布表(如图所示)
根据以上信息回答下列问题:
最喜爱的趣味运动项目类型频数分布表:
项目类型
频数
频率
跳绳
25
a
实心球
20
50m
b
0.4
拔河
0.15
(1)直接写出a= ,b= ;
(2)将图中的扇形统计图补充完整(注明项目、百分比);
(3)若全校共有学生1200名,估计该校最喜爱50m和拔河的学生共约有多少人?

相关试题

