搜索
【题目】在平行四边形ABCD中添加下列条件，不能判定四边形ABCD是矩形的是（ ）
A. 
90°B. AC
BDC. AC=BDD. 
参考答案：
【答案】B
【解析】
矩形的判定定理有：
（1）有一个角是直角的平行四边形是矩形；
（2）有三个角是直角的四边形是矩形；
（3）对角线相等的平行四边形是矩形．据此分析判断．
解：A、根据有一个角是直角的平行四边形是矩形能判定平行四边形ABCD为矩形，故此选项不符合题意；
B、不能判定平行四边形ABCD为矩形，故此选项符合题意；
C、根据对角线相等的平行四边形是矩形能判定平行四边形ABCD为矩形，故此选项不符合题意；
D、由平行四边形ABCD中AB∥CD，可得∠DCB+∠ADC=180°，又∠ADC =∠DCB，得出∠DCB=∠ADC=90°，根据有一个角是直角的平行四边形是矩形能判定平行四边ABCD为矩形，故此选项不符合题意；
故选：B．
-
科目： 来源： 题型：
查看答案和解析>>【题目】口袋中装有四个大小完全相同的小球，把它们分别标号1,2,3,4，从中随机摸出一个球，记下数字后放回，再从中随机摸出一个球，利用树状图或者表格求出两次摸到的小球数和等于4的概率.
【答案】
.【解析】试题分析：
根据题意列表如下，由表可以得到所有的等可能结果，再求出所有结果中，两次所摸到小球的数字之和为4的次数，即可计算得到所求概率.
试题解析：
列表如下：
1
2
3
4
1
（1，1）
（1，2）
（1，3）
（1，4）
2
（2，1）
（2，2）
（2，3）
（2，4）
3
（3，1）
（3，2）
（3，3）
（3，4）
4
（4，1）
（4，2）
（4，3）
（4，4）
由表可知，共有16种等可能事件，其中两次摸到的小球数字之和等于4的有（3，1）、（2，2）和（1，3），共计3种，
∴P（两次摸到小球的数字之和等于4）=
.【题型】解答题
【结束】
23【题目】小亮同学想利用影长测量学校旗杆AB的高度，如图，他在某一时刻立1米长的标杆测得其影长为1.2米，同时旗杆的投影一部分在地面上BD处，另一部分在某一建筑的墙上CD处，分别测得其长度为9.6米和2米，求旗杆AB的高度．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，AB为半圆O的直径，C为BA延长线上一点，CD切半圆O于点D。连结OD，作BE⊥CD于点E，交半圆O于点F。已知CE=12，BE=9,
(1)求证：△COD∽△CBE；
(2)求半圆O的半径的长
-
科目： 来源： 题型：
查看答案和解析>>【题目】关于一次函数y=﹣2x+3，下列结论正确的是（ ）
A. 图象过点（1，﹣1） B. 图象经过一、二、三象限
C. y随x的增大而增大 D. 当x＞
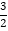时，y＜0 -
科目： 来源： 题型：
查看答案和解析>>【题目】如图，P为线段AB上的一个点，分别以AP，PB为边在AB的同侧作菱形APCD和菱形PBFE，点P，C，E在一条直线上。若∠DAP=60°，AP2+3PB2=1， M，N分别是对角线AC，BE的中点. MN长为（ ）
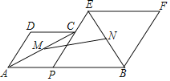
A.
B.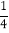 
C. 1D. 4 -
科目： 来源： 题型：
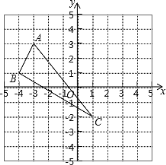
查看答案和解析>>【题目】在平面直角坐标系中，△ABC三个顶点的位置如图(每个小正方形的边长均为1)：
(1)请画出△ABC沿
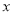轴向右平移3个单位长度，再沿
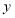轴向上平移2个单位长度后的
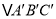(其中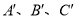
分别是A、B、C的对应点，不写画法)；(2)直接写出
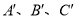三点的坐标；(3)求△ABC的面积．
-
科目： 来源： 题型：
查看答案和解析>>【题目】如图，正方形ABCD中，E、F分别是边AD、CD上的点，AE=ED，DF=
DC，连接EF并延长交BC的延长线于点G。（1）求证：△ABE∽△DEF；
（2）若正方形的边长为4，求BG的长。
相关试题
