【题目】如图,点P是AB上任一点,∠ABC=∠ABD,从下列各条件中补充一个条件,不一定能推出ΔAPC≌ΔAPD的是( )

A.BC=BD B.∠ACB=∠ADB C.AC=AD D.∠CAB=∠DAB
参考答案:
【答案】C
【解析】
试题分析:选项A,补充BC=BD,利用SAS先证出△ABC≌△ABD,可得∠CAB=∠DAB,AC=AD,再利用SAS即可得△APC≌△APD,选项A正确;选项B,补充∠ACB=∠ADB,利用AAS先证出△ABC≌△ABD,可得∠CAB=∠DAB,AC=AD,再利用SAS即可得△APC≌△APD,选项B正确;选项C,补充AC=AD,不能推出△APC≌△APD,选项C错误;选项D,补充∠CAB=∠DAB,利用ASA先证出△ABC≌△ABD,可得AC=AD,再利用SAS即可得△APC≌△APD,选项D正确.故答案选C.
-
科目: 来源: 题型:
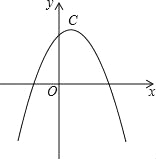
查看答案和解析>>【题目】若两条抛物线的顶点相同,则称它们为“友好抛物线”,抛物线C1:y1=﹣2x2+4x+2与C2:u2=﹣x2+mx+n为“友好抛物线”.
(1)求抛物线C2的解析式.
(2)点A是抛物线C2上在第一象限的动点,过A作AQ⊥x轴,Q为垂足,求AQ+OQ的最大值.
(3)设抛物线C2的顶点为C,点B的坐标为(﹣1,4),问在C2的对称轴上是否存在点M,使线段MB绕点M逆时针旋转90°得到线段MB′,且点B′恰好落在抛物线C2上?若存在求出点M的坐标,不存在说明理由.
-
科目: 来源: 题型:
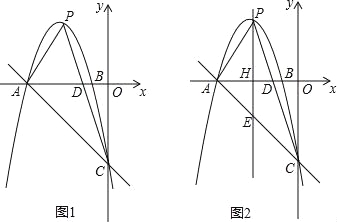
查看答案和解析>>【题目】如图1,抛物线y=ax2﹣6x+c与x轴交于点A(﹣5,0)、B(﹣1,0),与y轴交于点C(0,﹣5),点P是抛物线上的动点,连接PA、PC,PC与x轴交于点D.
(1)求该抛物线所对应的函数解析式;
(2)若点P的坐标为(﹣2,3),请求出此时△APC的面积;
(3)过点P作y轴的平行线交x轴于点H,交直线AC于点E,如图2.
①若∠APE=∠CPE,求证:=;
②△APE能否为等腰三角形?若能,请求出此时点P的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】正方形具有而菱形不一定具有的性质是( ).
A. 对角线互相垂直 B. 对角线互相平分
C. 对角线相等 D. 对角线平分一组对角
-
科目: 来源: 题型:
查看答案和解析>>【题目】解不等式,并把解集在数轴上表示出来.
10-4(x-3)≤2(x-1).
-
科目: 来源: 题型:
查看答案和解析>>【题目】已知一个多边形的内角和为540°,则这个多边形为
A、三角形B、四边形C、五边形D、六边形
-
科目: 来源: 题型:
查看答案和解析>>【题目】抛物线y=x2+1过两点A(﹣2,y1)和B(3,y2),则y1y2(填>,<,=).
相关试题

