【题目】如图,O是直线AC上一点,OB是一条射线,OD平分∠AOB,OE在∠BOC内部,∠BOE=![]() ∠EOC,∠DOE=70°,求∠EOC的度数.
∠EOC,∠DOE=70°,求∠EOC的度数.

参考答案:
【答案】80°
【解析】
设∠BOE=x°,则∠EOC=2x°,由∠DOE=70°,OD平分∠AOB知,∠AOD=∠DOB=70°﹣x°,再根据∠AOD+∠DOB+∠BOE+∠EOC=180°,列出关于x的方程求解即可.
解:如图,设∠BOE=x°,
∵∠BOE=![]() ∠EOC,
∠EOC,
∴∠EOC=2x°,
∵OD平分∠AOB,
∴∠AOD=∠DOB=70°﹣x°,
∵∠AOD+∠DOB+∠BOE+∠EOC=180°,
∴70°﹣x°+70°﹣x°+x°+2x°=180°,
∴x°=40°,
∴∠EOC=80°.
“点睛”本题主要考查角的计算及角平分线的定义,熟练掌握角平分线的定义及性质是解题的关键.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,等边△ABC的边长为6,点D为AB上一点,DE⊥BC于点E,EF⊥AC于点F,连接DF.若△DEF也是等边三角形,求AD的长.
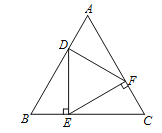
-
科目: 来源: 题型:
查看答案和解析>>【题目】上海世博会会期为2010年5月1日至2010年10月31日。门票设个人票和团队票两大类。个人普通票160元/张,学生优惠票100元/张;成人团队票120元/张,学生团队票50元/张。
(1)如果2名老师、10名学生均购买个人票去参观世博会,请问一共要花多少元钱购买门票?
(2)用方程组解决下列问题:如果某校共30名师生去参观世博会,并得知他们都是以团队形式购买门票,累计花去2200元,请问该校本次分别有多少名老师、多少名学生参观世博会?
-
科目: 来源: 题型:
查看答案和解析>>【题目】某一工程,在工程招标时,接到甲、乙两个工程队的投标书.甲工程队施工一天,需付工程款1万元;乙工程队施工一天,需付工程款0.6万元.根据甲、乙工程队的投标书测算,可有三种施工方案:
(A)甲队单独完成这项工程,刚好如期完成;
(B)乙队单独完成这项工程要比规定工期多用4天;
(C)若甲、乙两队合做3天后,剩下的工程由乙队单独做,也正好如期完工.
为了节省工程款,同时又能如期完工,你认为应选择哪一种方案?并说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】小虫从某点o出发在一条直线上来回爬行,假定向右爬行的路程记为正数,向左爬行的路程记为负数,爬过的各段路程(单位:厘米)依次为
 ,
,




 通过计算说明小虫是否回到起点?如果小虫爬行的速度0.5厘米/秒,小虫共爬行了多少时间?
通过计算说明小虫是否回到起点?如果小虫爬行的速度0.5厘米/秒,小虫共爬行了多少时间? -
科目: 来源: 题型:
查看答案和解析>>【题目】杨梅是漳州的特色时令水果,杨梅一上市,水果店的老板用1200元购进一批杨梅,很快售完;老板又用2500元购进第二批杨梅,所购件数是第一批的2倍,但进价比第一批每件多了5元.
(1)第一批杨梅每件进价多少元?
(2)老板以每件150元的价格销售第二批杨梅,售出80%后,为了尽快售完,决定打折促销,要使第二批杨梅的销售利润不少于320元,剩余的杨梅每件售价至少打几折?(利润=售价﹣进价) -
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,在菱形ABCD中,对角线AC与BD相交于点O,AB=13,BD=24,在菱形ABCD的外部以AB为边作等边三角形 ABE.点F是对角线BD上一动点(点F不与点B重合),将线段AF绕点A顺时针方向旋转60°得到线段AM,连接FM.

(1)求AO的长;
(2)如图2,当点F在线段BO上,且点M,F,C三点在同一条直线上时,求证:AC= AM;
AM;
(3)连接EM,若△AEM的面积为40,请直接写出△AFM的周长.
温馨提示:考生可以根据题意,在备用图中补充图形,以便作答
相关试题

