Question

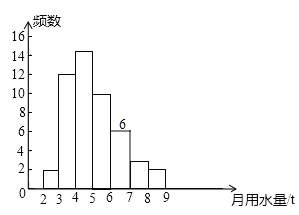
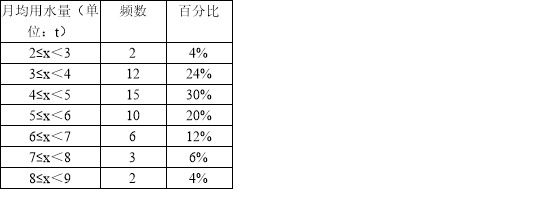
【题目】（7分）小军同学在学校组织的社会调查活动中负责了解他所居住的小区450户居民的生活用水情况，他从中随机调查了50户居民的月均用水量（单位：t），并绘制了样本的频数分布表和频数分布直方图（如图）．

（1）请根据题中已有的信息补全频数分布表和频数分布直方图；

（2）如果家庭月均用水量“大于或等于4t且小于7t”为中等用水量家庭，请你通过样本估计总体中的中等用水量家庭大约有多少户？

（3）从月均用水量在2≤x＜3，8≤x＜9这两个范围内的样本家庭中任意抽取2个，求抽取出的2个家庭来自不同范围的概率．

Answer 1

【答案】（1）4≤x＜5的户数是：15，所占的百分比是：30%，6≤x＜7部分调查的户数是：6，作图见试题解析；（2）279；（3）．

【解析】

试题分析：（1）根据第一组的频数是2，百分比是4%即可求得总人数，然后根据百分比的意义求解；

（2）利用总户数540乘以对应的百分比求解；

（3）在2≤x＜3范围的两户用a、b表示，8≤x＜9这两个范围内的两户用1，2表示，利用树状图法表示出所有可能的结果，然后利用概率公式求解．

试题解析：（1）调查的总数是：2÷4%=50（户），则6≤x＜7部分调查的户数是：50×12%=6（户），

则4≤x＜5的户数是：50﹣2﹣12﹣10﹣6﹣3﹣2=15（户），所占的百分比是：×100%=30%．

（2）中等用水量家庭大约有450×（30%+20%+12%）=279（户）；

（3）在2≤x＜3范围的两户用a、b表示，8≤x＜9这两个范围内的两户用1，2表示．

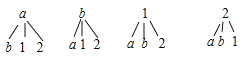
则抽取出的2个家庭来自不同范围的概率是：=．