【题目】在平面直角坐标系中,点O为原点,平行于x轴的直线与抛物线L:![]() 相交于A,B两点(点B在第一象限),点D在AB的延长线上.
相交于A,B两点(点B在第一象限),点D在AB的延长线上.
(1)已知a=1,点B的纵坐标为2.
①如图1,向右平移抛物线L使该抛物线过点B,与AB的延长线交于点C,求AC的长.
②如图2,若BD=![]() AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
AB,过点B,D的抛物线L2,其顶点M在x轴上,求该抛物线的函数表达式.
(2)如图3,若BD=AB,过O,B,D三点的抛物线L3,顶点为P,对应函数的二次项系数为a3,过点P作PE∥x轴,交抛物线L于E,F两点,求![]() 的值,并直接写出
的值,并直接写出![]() 的值.
的值.

参考答案:
【答案】(1)①![]() ;②
;②![]() ;(2)
;(2)![]() ,
,![]() .
.
【解析】
试题分析:(1)①根据函数解析式求出点A、B的坐标,求出AC的长;
②作抛物线L2的对称轴与AD相交于点N,根据抛物线的轴对称性求出OM,利用待定系数法求出抛物线的函数表达式;
(2)过点B作BK⊥x轴于点K,设OK=t,得到OG=4t,利用待定系数法求出抛物线的函数表达式,根据抛物线过点B(t,![]() ),求出
),求出![]() 的值,根据抛物线上点的坐标特征求出
的值,根据抛物线上点的坐标特征求出![]() 的值.
的值.
试题解析:(1)①二次函数![]() ,当y=2时,2=
,当y=2时,2=![]() ,解得
,解得![]() ,
,![]() ,∴AB=
,∴AB=![]() .
.
∵平移得到的抛物线L1经过点B,∴BC=AB=![]() ,∴AC=
,∴AC=![]() .
.
②作抛物线L2的对称轴与AD相交于点N,如图2,根据抛物线的轴对称性,得BN=![]() DB=
DB=![]() ,∴OM=
,∴OM=![]() .
.
设抛物线L2的函数表达式为![]() ,由①得,B点的坐标为(
,由①得,B点的坐标为(![]() ,2),∴
,2),∴![]() ,解得a=4.∴抛物线L2的函数表达式为
,解得a=4.∴抛物线L2的函数表达式为![]() ;
;
(2)如图3,抛物线L3与x轴交于点G,其对称轴与x轴交于点Q,过点B作BK⊥x轴于点K,设OK=t,则AB=BD=2t,点B的坐标为(t,![]() ),根据抛物线的轴对称性,得OQ=2t,OG=2OQ=4t.
),根据抛物线的轴对称性,得OQ=2t,OG=2OQ=4t.
设抛物线L3的函数表达式为![]() ,∵该抛物线过点B(t,
,∵该抛物线过点B(t,![]() ),∴
),∴![]() ,∵t≠0,∴
,∵t≠0,∴![]() ,由题意得,点P的坐标为(2t,
,由题意得,点P的坐标为(2t,![]() ),则
),则![]() ,解得:
,解得:![]() ,
,![]() ,EF=
,EF=![]() ,∴
,∴![]() .
.
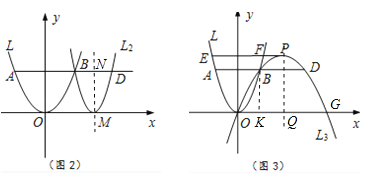
-
科目: 来源: 题型:
查看答案和解析>>【题目】阅读:如图1,点P(x,y)在平面直角坐标中,过点P作PA⊥x轴,垂足为A,将点P绕垂足A顺时针旋转角α(0°<α<90°)得到对应点P′,我们称点P到点P′的运动为倾斜α运动.例如:点P(0,2)倾斜30°运动后的对应点为P′(1,
 ).
).图形E在平面直角坐标系中,图形E上的所有点都作倾斜α运动后得到图形E′,这样的运动称为图形E的倾斜α运动.
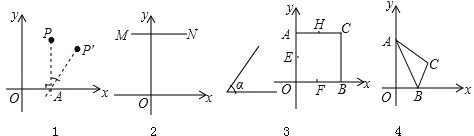
理解
(1)点Q(1,2)倾斜60°运动后的对应点Q′的坐标为 ;
(2)如图2,平行于x轴的线段MN倾斜α运动后得到对应线段M′N′,M′N′与MN平行且相等吗?说明理由.
应用:(1)如图3,正方形AOBC倾斜α运动后,其各边中点E,F,G,H的对应点E′,F′,G′,H′构成的四边形是什么特殊四边形: ;
(2)如图4,已知点A(0,4),B(2,0),C(3,2),将△ABC倾斜α运动后能不能得到Rt△A′B′C′,且∠A′C′B′为直角,其中点A′,B′,C′为点A,B,C的对应点.请求出cosα的值.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图1,抛物线
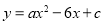 与x轴交于点A(﹣5,0)、B(﹣1,0),与y轴交于点C(0,﹣5),点P是抛物线上的动点,连接PA、PC,PC与x轴交于点D.
与x轴交于点A(﹣5,0)、B(﹣1,0),与y轴交于点C(0,﹣5),点P是抛物线上的动点,连接PA、PC,PC与x轴交于点D.(1)求该抛物线所对应的函数解析式;
(2)若点P的坐标为(﹣2,3),请求出此时△APC的面积;
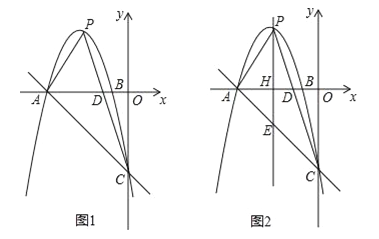
(3)过点P作y轴的平行线交x轴于点H,交直线AC于点E,如图2.
①若∠APE=∠CPE,求证:
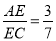 ;
;②△APE能否为等腰三角形?若能,请求出此时点P的坐标;若不能,请说明理由.
-
科目: 来源: 题型:
查看答案和解析>>【题目】等腰三角形ABC中,一腰AB的垂直平分线交另一腰AC于G,已知AB=10,△GBC的周长为17,则底BC为( )
A.5
B.7
C.10
D.9 -
科目: 来源: 题型:
查看答案和解析>>【题目】如图,小贤为了体验四边形的不稳定性,将四根木条用钉子钉成一个矩形框架ABCD,B与D两点之间用一根橡皮筋拉直固定,然后向右扭动框架,观察所得四边形的变化,下列判断错误的是( )
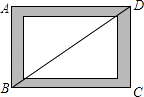
A.四边形ABCD由矩形变为平行四边形
B.BD的长度增大
C.四边形ABCD的面积不变
D.四边形ABCD的周长不变 -
科目: 来源: 题型:
查看答案和解析>>【题目】把一个图形绕着某一点旋转________,如果它能够与另一个图形重合,那么就说这两个图形关于这个点对称或________,这个点叫做它们的________.这两个图形在旋转后能重合的对应点叫做关于对称中心的________.
-
科目: 来源: 题型:
查看答案和解析>>【题目】如图,△ABC与△ADE都是等腰直角三角形,∠C和∠AED都是直角,点E在AB上,如果,△ABC旋转后能与△ADE重合,那么哪一点是旋转中心?旋转了多少度?
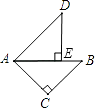
相关试题

