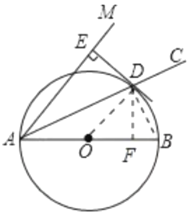
【题目】如图，为平分线，，以的长为直径作交于点，过点作于点．

（1）求证：是的切线．

（2）若，的长=_____．

【答案】（1）见解析；（2）

【解析】

（1）连接OD，根据AC为∠BAM的平分线以及OA=OD得到∠MAC＝∠ADO，从而得出AE∥OD，结合DE⊥AM即可解答．
（2）过点D作DF⊥AB于点F，即可证得DE＝DF＝6，在Rt△ADF中利用射影定理求得AF，然后利用勾股定理求出AD．

（1）证明：连接OD，
∵AC为∠BAM的平分线，
∴∠BAC＝∠MAC，
∵OA＝OD，
∴∠BAC＝∠ADO，
∴∠MAC＝∠ADO
∴AE∥OD，
∵DE⊥AM，
∴OD⊥DE，
∴DE是⊙O的切线；
（2）解：连接BD，过点D作DF⊥AB于点F，
∵AC为∠BAM平分线，DE⊥AM，
∴DF＝DE＝6，
∵AB是直径，，
∴∠ADB＝90°，
∴DF2＝AFBF，即62＝AF（13AF），
∴AF＝9或AF＝4（舍去）
∴AD＝．

故答案为：．

关闭